About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators2次方程式 例題 2次方程式の解き方(因数分解利用) 2次方程式の解き方(解の公式利用) 解から2次方程式を求める1 解から2次方程式を求める2 2次方程式文章題 数の問題 2次方程式文章題 図形の問題 2次方程式文章題 動点 2次方程式文章題 座標 2次方程式文章題 割合二次方程式の解き方はバッチリになりましたか? 二次方程式は解き方がたくさんあるので、ちょっと難しく感じる方もいるかもしれません。 苦手な方は、とにかく演習あるのみです! 問題を眺めているだけでは、解き方は身につきません。

2 5一元二次方程及其解法
二次方程式 文章題 例題
二次方程式 文章題 例題-2次方程式 例題 2次方程式の解き方(因数分解利用) 2次方程式の解き方(解の公式利用) 解から2次方程式を求める1 解から2次方程式を求める2 2次方程式文章題 数の問題 2次方程式文章題 図形の問題 2次方程式文章題 動点 2次方程式文章題 座標 2次方程式文章題 割合二次方程式因数分解を利用した解き方を例題解説! kaztastudy 今回は、中3で学習する二次方程式の単元から 因数分解を利用して計算する方法 について解説していくよ!



中考数学一元二次方程的解法精选例题解析 中考 学习资料大全 免费学习资源下载
二次方程式の解き方をたくさん勉強してきた。 因数分解をつかった解き方とか、 解の公式でとくやり方とかね。 ぶっちゃけ、 どんな二次方程式もとける自信あるよね?? だがしかし、中3数学の二次方程式はまだこれからなんだ。 二次方程式のゴールは、 定数分離の応用例1(二次関数・解の条件) まずは,例題を通じて定数分離とは何か説明します。 例題1 x x x についての二次方程式 x 2 − 2 x − a = 0 x^22xa=0 x2 −2x −a = 0 が − 1 1 −1 以上の異なる実数解を二つ持つための ここではこんなことを紹介しています↓ 天才数学者ロー氏が考案した二次方程式や因数分解に使える新しい解き方を紹介しています。 この解法の特徴としては、 あの覚えづらい解の公式を使わずに解けてしまう 比較的簡単である ということです。 何より、「なるほどね」と思える面白い発
次の式 y''P(x)y'Q(x)y=0 を「2階線形同次微分方程式」というのに対して, y''P(x)y'Q(x)y=R(x) を「2階線形非同次微分方程式」といいます. 定数係数の2階線形微分方程式については,同次方程式は次の(1)の形,非同次方程式は(2)の形になります.( a, b は定数の係数)2次方程式 例題 2次方程式の解き方(因数分解利用) 2次方程式の解き方(解の公式利用) 解から2次方程式を求める1 解から2次方程式を求める2 2次方程式文章題 数の問題 2次方程式文章題 図形の問題 2次方程式文章題 動点 2次方程式文章題 座標 2次方程式文章題 割合2次方程式の平方完成による解法 例題 練習問題 2次方程式の解の公式による解法 例題 練習問題 2次方程式の実数解の個数 (判別式) 例題 練習問題 文字係数の連立方程式の説明 例題 練習問題 方程式・不等式の応用として 不定方程式 例題1 例題 2 練習問題
二次方程式の解と係数の関係を,2つの方法で証明しました。 解の公式を使う方法 因数定理を使う方法 実は,解と係数の関係は,3次以上の高次方程式の場合にも拡張できる美しい公式です。→三次,四次,n次方程式の解と係数の関係とその証明 二次不定方程式$\ ax^2bxycy^2dxeyf=0\ $の解き方 この形の不定方程式は、$\ ax^2bxycy^2dxeyf\ $を因数分解する方針で解けることもあります。 しかし、これはうまくいかないときもあるのでオススメできません。 上記の例題で述べた組立除法のやり方を整理します。 割られる多項式が三次式 f (x) = a 3 x 3 a 2 x 2 a 1 x a 0 f(x)=a_3x^3a_2x^2a_1xa_0 f (x) = a 3 x 3 a 2 x 2 a 1 x a 0 の場合を考えます。一般の n n n 次式の場合も全く同じです。




綜 一元二次方程式應用問題 考題 台灣數位學苑 K12 數學



齊次微分方程 Lyu Cing Yu Wed
二次方程式を解くアプリ! aX2 bX c = 0 で表される一般的な二次方程式で、係数 a, b, c を入力すると、X の値を求めてくれます。 まず式を aX2 bX c = 0 の形に整理して下さい。 ( a, b, c の値は整数で ) 次に、a, b, c の値を入力し、「解く」をクリックし二次関数 2次方程式の解の存在範囲判・軸・端の条件を見極めるのが重要! kaztastudy例題 例題1 (1) 次の方程式のうち、 tについての二次方程式であるものを選 び、記号で答えなさい。 (ア) t e3 l0 (イ) 5 l f6 6 (ウ) 05 66 (2) 2、1、0、1、2のうち、二次方程式 t 6 f t2 l0の解は




高等数学 非齐次线性微分方程解的结构 含例题解析 寒泉 Csdn博客 非齐次线性微分方程解的结构




解一元二次方程公式法
2次方程式(因数分解利用) 基礎 AB=0なら、A=0またたB=0 この考え方をつかって2次方程式を解く。 例題 x 2 8x = 0 左辺を因数分解する。 x(x8)= 0 積が0になるのは2つの因数のうちどちらかが0なので x=0, または x8=0 よって x=0, 8 x 2 x = 6 二つ目の因数から出てくる二次方程式の解と合わせると答えは x = 1 2, ± 6 2 x=\dfrac{1}{2},\pm\dfrac{\sqrt{6}}{2} x = 2 1 , ± 2 6 補足 この問題は有理数解の候補がたくさんある中で当たりが一つしかないので解きにくい問題です。2次方程式と2次関数についての説明です。教科書「数学I」の章「関数と方程式・不等式」の中の文章です。 『2次方程式の解法』の例題では、因数分解を利用して解いた2次方程式 $3x^22x8=0$ を、今度は平方完成を使って解いてみよう。




2 3b例題02四次方程式的所有根含虛數根 務必要有耐心 數學 均一教育平台




根與係數關係三次根與系數的關系 百度百科 Gquhm
例題1: sin θ = 1 2 を、 0 ≤ θ < 2 π の範囲で解け。 すでに sin = という形になっており、手順1は完了しています。 単位円と y = 1 2 の交点に対応する角度が答えです。 これを求めると、 θ = π 6, 5 6 π です。 ~補足~数学 A 2次方程式 例題18 14中考数学填空题练习 一元二次方程b 子供向けぬりえ ロイヤリティフリー2元1次方程式题目 一元二次方程解法 公式法 初中数学 彩色时客 一元二次方程的有理根与整数根精选压轴题演练 助战中考 收藏 一元二次方程因式分解法 重解とは? 重解とは、 高次方程式の \(\bf{2}\) つ以上の解が同じになる(= 解が重なる)こと です。 一般に、\(n\) 次方程式は \(n\) 個の解をもちますが、そのうちのいくつかの解が同じ値となるとき、その解を「重解」と呼びます。 二次方程式を例に考えてみましょう。




2 二元三次方程式




教科書要改了 一元二次方程的 極簡 解法比求根公式更簡單 人人焦點




平方根解法配方法解一元二次方程式一元二次方程式的公式解 Ppt Download




中考數學 一元二次方程典型綜合題原創詳析 驚嘆數學變形之精妙 壹讀




二元二次方程的例题 二元二次方程组的例题和解法 三人行教育网 Www 3rxing Org



12中考数学精选例题解析 一元二次方程根的判别式 中考数学 中考网



一元二次方程公式法 万图壁纸网
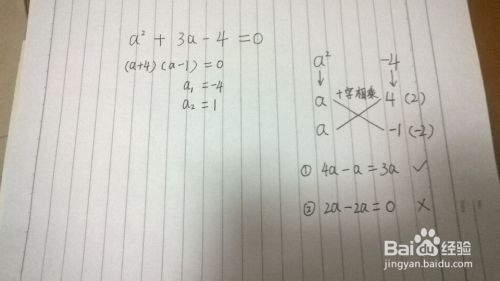



巧用十字相乘法解一元二次方程 图文解释 百度经验




想請問什麼是複數係數一元二次方程式 Clear



韦达定理 一元二次方程根与系数的关系 新华网
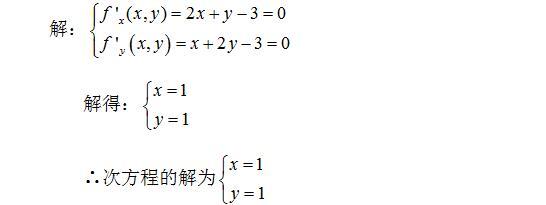



二元二次方程的解法 知乎



换元法解方程例题讲解3 换元法 奥数网




一元二次方程计算题 搜索结果 哔哩哔哩弹幕视频网 つロ乾杯 Bilibili




巧用十字相乘法解一元二次方程 图文解释 百度经验




例題 一元二次應用題 果園面積 Youtube




一元二次方程及其解法 一 直接开平方法 知识讲解 基础 下载 Word模板 爱问共享资料



Q Tbn And9gctp9xemhcqd7pbjtxvjw6dgrcg91nx31cnercrp8x7c2yt H Usqp Cau




2 5一元二次方程及其解法




2 5一元二次方程及其解法



中考数学一元二次方程的解法精选例题解析 中考 学习资料大全 免费学习资源下载




初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 101教育知识点频道手机端



基提尖 第十三讲笔记 一元二次方程根系关系 学而思卢老师 微信公众号文章阅读 Wemp



一阶微分方程例题 搜狗图片搜索



公式法解一元二次方程的例题 初三网




2次方程式の解の公式による解法 数学i フリー教材開発コミュニティ Ftext




トップ100連立方程式公式 最高のカラーリングのアイデア



初中数学知识例题点讲解 一元二次方程 代数辅导 中考网



初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 学阅网知识点频道



初中数学知识点总结 一元二次方程的应用 学习云课堂




一元二次方程求根公式




中学3年生 数学 2次方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



精品 一元二次方程典型例题整理版 松鼠文库




初中數學 一元二次方程的常見考點 你都掌握了哪些 每日頭條




1 2一元二次方程式 例題3 動態解題 Youtube



一元二次方程的解法合辑 图片信息欣赏 图客 Tukexw Com



齊次微分方程 Lyu Cing Yu Wed




判別式判別式 Ynf




雙二次方程 定義 求方程的解 無實數解情形 求解步驟 注意事項 典型例題 例1 例 中文百科全書



例 判別式 台灣數位學苑 K12 數學



一元二次方程配方法 4道提高题 全做对你就是学霸水平 初中 Qq教育网



解一元一次方程50道练习题 经典 强化 带答案 松鼠文库




例題7 利用乘法公式解一元二次方程式 Youtube



十字相乘法因式分解解一元二次方程 哔哩哔哩 つロ干杯 Bilibili




例題複數一元二次方程式1 Youtube




复数系数一元二次方程的根的问题 21世纪教育网



Www Sdime Ntnu Edu Tw Uploads Asset Data 5da8cb1b1d41c8017f0039c9 E5 85 Ab E4 B8 8a E7 Ac Ac E5 9b 9b E7 Ab A0 E5 96 Ae E5 85 E4 Ba 94 Pdf




一元二次方程的有理根与整数根精选压轴题演练 助战中考 收藏




例題 先將乘積展開後再求解 數學 均一教育平台




2 3a觀念06一元二次方程式的判別式之討論 數學 均一教育平台
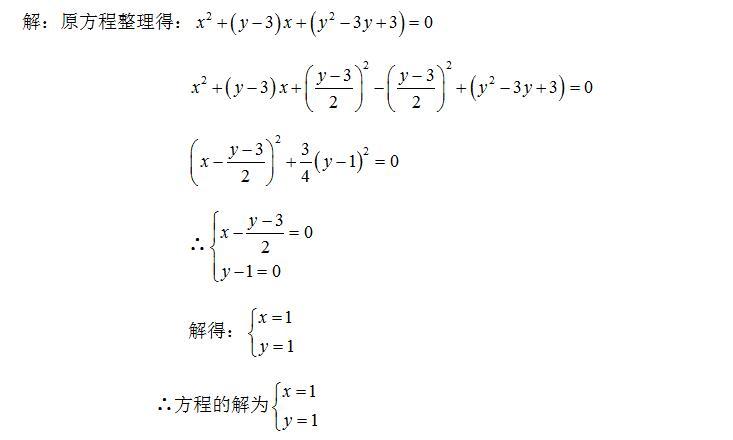



二元二次方程的解法 知乎



一元二次方程练习题 附答案 职场达人网 职场知识 职场礼仪 职场法则



中考數學一元二次方程根的判別式精選例題解析 愛經驗



含参一元二次方程有实数根 求含参字母k取值范围 中考数学常考 哔哩哔哩 Bilibili




一元二次方程的解法 公式法 因式分解法和十字相乘法基础练习 一元二次方程交叉相乘 艾帝网




2 5一元二次方程及其解法



韦达定理负数 一元二次方程根与系数的关系 韦达定理 尚书坊




一元二次方程的解法公式有哪些 一元二次方程的图像 星火网校



Q Tbn And9gctivnh0ytvm5iq2nnhaeu2fa7uykcwky0 V7mocdeysfgddbodx Usqp Cau




怎么解一元二次方程式




例題 用配方法解方程 二次項係數為負 Youtube




二元二次方程的解法 知乎




方程与不等式下载 Word模板 爱问共享资料




例題8 利用配方法解一元二次方程式3 常數項很大 Youtube




一般的一元二次方程的解法 直接开平方法 因式分解法 知识讲解 快资讯



2



一元二次方程 万图壁纸网



九年级上 一元二次方程根的判别式确定未知字母的取值 九年级 老杨的博客



一元二次方程求根公式练习题 初三网



初中数学知识点总结 一元二次方程的应用 易贤网



Ex 公式解 一元二次方程式 發現學習的美麗新世界




初中数学一元二次方程求根公式 一元二次方程的解法 一元二次方程根与系数的关系 101教育知识点频道手机端




多項式的微積分 维基教科书 自由的教学读本



一元二次方程题目 万图壁纸网



一元二次方程考点透视 第52周 综合复习 初中人教五四制 数学中国网




配方法例子 大家都在找解答 訂房優惠報報



一元二次方程的根与系数的关系




例題11 利用公式解解一元二次方程式 重根和無解 Youtube




第二章 2 1 微分方程 差分方程求解 举例 Einstellung的博客 Csdn博客



公式法解一元二次方程的例题 初三网




最も欲しかった 数学2 次方程式 ニスヌーピー壁紙



1




一道加拿大數學奧賽題 解三元二次方程組 正確率不到5 壹讀



一元二次方程的解法 配方法 知識講解 提高 雪花新闻




例 解一元二次方程式 2 台灣數位學苑 K12 數學




平方根解法配方法解一元二次方程式一元二次方程式的公式解 Ppt Download



12中考数学精选例题解析 二元二次方程组 中考数学 中考网




一元二次方程及其解法 一 直接开平方法 知识讲解 基础 下载 Word模板 爱问共享资料




因式分解



1




二次方程式公式解一元二次方程 Ejthgg



公式法解一元二次方程的例题 初三网




初中一元二次方程根的判別式的綜合應用 幫你解決中考最怕題型 每日頭條
(%E3%80%80)%E2%97%8F.png)



解方程




二元二次二元二次方程 Lvai



初中数学一元二次方程的判别式和根与系数的关系及例题讲解 初中数学 学习资料大全 免费学习资源下载




初中数学解一元二次方程 四种解法各有不同 学会灵活运用 每日头条




詳細實用的解方程方法總結 人人焦點



一元二次方程最重要应用题 商品销售问题 一节课彻底掌握 件数



0 件のコメント:
コメントを投稿