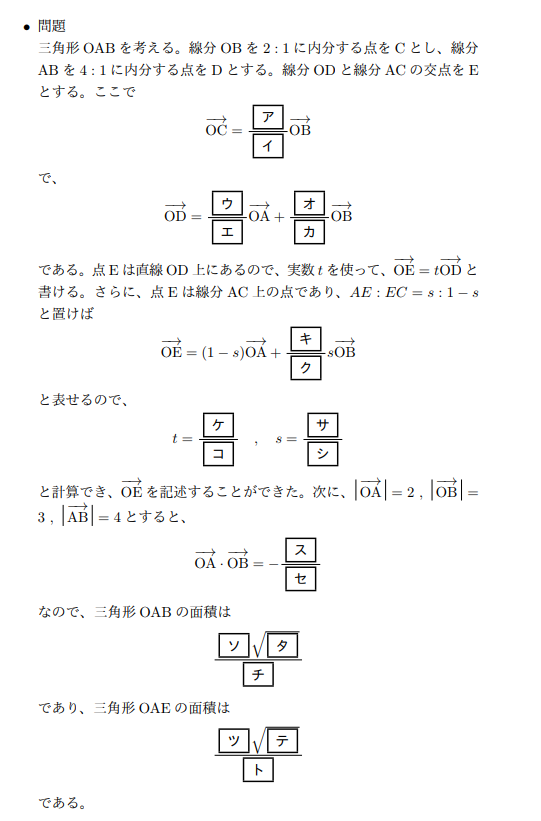
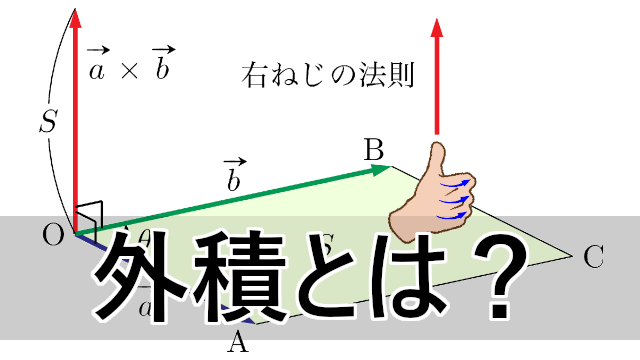
これは,\ {「2つのベクトルa,\ bが平行ならば面積は0になる」}という当たり前のことを意味する 高校数学で最も鬱陶しい公式の1つだが,\ 以下の三角形の面積の公式は要暗記である Aが原点となるよう3点を平行移動}すると\ {座標平面上の3点が与えられたとき四辺形の面積⃗a⃗bsinθ(θ はベクトル⃗aと⃗bの間に角)に等しい。(2) 方向と向きは、ベクトル⃗aと⃗bとに垂直で⃗aから⃗bへ右ネジを廻すときに ネジの進む方向。 その時に、次の分配法則等が成り立つ。 (1)⃗a×⃗b = −⃗b×⃗a,⃗a×⃗a = 0 (2)⃗a×(⃗b⃗c) =⃗a×⃗b⃗a×⃗c ベクトルの定番問題を一瞬で解く公式 上記と同様の議論を四面体に適用することにより以下の公式が得られます: 三角形の面積を求める公式

平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
ベクトル 面積 公式
ベクトル 面積 公式-AC)2 である。 A B C S (proof)\ABC = とおくと数学I の図形と計量の分野で学習する三角形の面積の公式より S= 1 2 j!172 ベクトル場の面積分を定義するには何がわかればよいか ベクトル場の線積分のときと同じように、ベクトル場の面積分もスカラー場の面積分を通じて定 義します。つまり、 • 曲面S からS を定義域とするベクトル場⃗n を上手く作る。
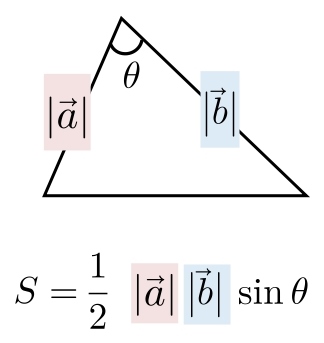



高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト
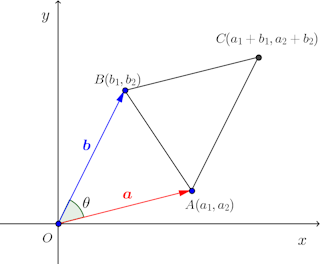
平面と空間の図形(内積, 外積の利用) 《要旨》外積を定義し, 内積, 外積と関連させて「基本図形の面積, 体積」や「空間内の直線, 平面」を取り扱う 《表記や用語の注意》 • 高校教科書ではベクトルを Ñ a " pa1,a2q (矢印, 横並びの成分) の形で表したが, 大学ではa " a1 a2 (太字,< 平面のベクトルと行列式> 原点を始点とする2つのベクトル a = ³ a1 a2 ´ ,b = ³ b1 b2 ´ に対して,原点O(0,0)と3点 A(a1,a2),B(b1,b2),C(a1 b1,a2 b2) をとると,四角形OACB は平行四辺形となる。 この平行四辺形の面積をS とする。aとbの位置関係が 図1のようなを満たすベクトルの組e1, e2, e3 を正規直交基底という このとき, (117) における基底ベクトルei の係数ai をベクトルaのこの基底に関する第i 成分という ベクトルの成分をもちいるとベクトルの長さは a = √ a2 1 a2 2 a2 3 (119) と表され, また, 内積は a·b = a1b1
正射影ベクトルの公式は?平面や空間での入試問題を東大医学部生が解説! この記事を読むとわかること ・正射影ベクトルがどういうものか ・平面における直線の上への正射影ベクトルの公式 ・空間における平面の上への正射影ベクトル 21年2月19日 この記事では、「ベクトルを使った三角形の面積の求め方」について、できるだけわかりやすく解説していきます。 公式の証明や計算問題なども解説していきますので、この記事を通してぜひマスターしてくださいね。 目次 非表示 空間ベクトルの公式は「空間ベクトル 公式一覧」で説明しているので、チェックしてみてください。 問題集を解く際の参考にしてください! 高校数学B平面ベクトル 公式一覧(内分・外分・面積) 学校よりわかりやすいサイト
応用ベクトルの等式と三角形の面積比 17年9月19日 年5月27日 ここでは、ベクトルの等式から三角形の面積比を求める問題を見ていきます。空間ベクトル 四面体の体積 2次元平面で、三角形の面積を求めるのにこのような公式を使いますが、 3次元空間ではどうなんだろうと思って、四面体の体積を計算してみましたところ、このような式シートの面積である.曲線Cに沿った線積分は,Aから測った曲線の長さをsとする と,次のように書くことができる. I = ˇ C f(x,y)ds = lim Δs→0 N i=1 f(x i,y i)Δs (311) ここで(x i,y i)はCを細かくN 等分し折れ線で近似した時のC上の点の座標で,折れ
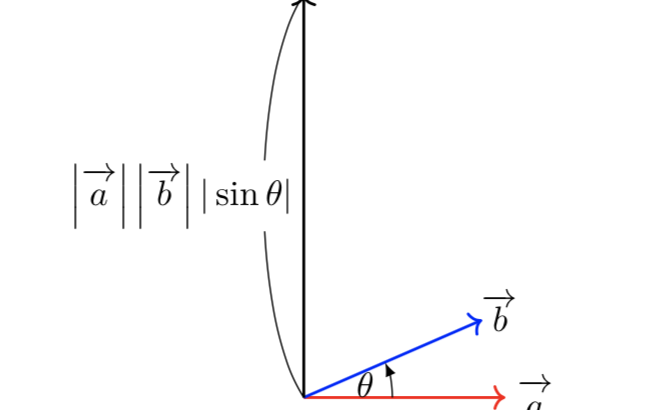



ベクトルの外積の公式やその覚え方とは 高校範囲で役立つ場面についても解説 東大医学部生の相談室



正四面体とベクトルの面積公式 難関大学への数学
ベクトルと三角形の面積の公式 三角形の面積の公式 その1 4ABCの面積Sについて S= 1 2 q j!はじめに ここでは、ベクトルを用いた三角形の面積の求め方、その公式について説明しています。 面積を求める公式 図のように、 と で張られる三角形の面積をSとします。 このとき、面積Sは、次のように表すことができます。 これをベクトルの外積 ここでは,ベクトルの外積(ベクトル積) は物理学でよく使われる3次元ベクトルに対してのみ考えるものとする. (1) 図形による定義 ベクトルの外積 の向きは,ベクトル の向きからベクトル の向きへ右ネジを回転させたとき,ネジの




ヘロンの公式 東大合格コム




勉強しよう数学 三角形の面積をベクトルで分解して計算する
ベクトル解析 公式一覧 on Math 高専4年の数学の教科書として使用した「新 応用数学」(大日本図書) のベクトル解析についての公式などを備忘録としてまとめたものです。 ベクトルの外積 (裏技)による法線ベクトル・空間の三角形の面積・平行六面体の体積・四面体の体積 ベクトルの外積は受験数学最強の裏技の1つであり,\ 上級者は是非習得しておいてほしい 大学1年の最初に学習する程度の知識であり,\ 適用できる試験問題ベクトルの平行条件,垂直条件 3点が一直線上にある条件 → 携帯版は別頁 == 三角形の重心,内心,外心,垂心 (ベクトル,三角関数) == このページで解説する内容 各々その項目をクリックすれば解説にジャンプします 原点を O とし, ABC の頂点の位置




高校数学の ベクトル 内積 三角形の面積公式 に関する問題を解いてみる Yahoo 知恵袋より Makelemonadejp Com



空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典
ベクトルの三角形の面積の公式について 回答 そうですよね。 確かに覚えにくいですよね。 でも、これって簡単に導けるんですよ。 数学の公式って、全て暗記しようとする人が多いですが、覚えるべき公式とそうでない公式を区別した方がいいですよ ベクトルの定番問題の公式(面積比) 超頻出です。三角形の五心の座標を表すのに応用することも。 三角形の面積比にまつわる公式たち 中学数学チックな公式です。チェバの定理の証明に応用したり三次元に拡張したり。 複素数平面における三角形の面積このように、ベクトルの外積 →v × →w とは、2つのベクトル →v と →w が作る平行四辺形に対して垂直方向に伸びる新しいベクトルなのです。




6 柱と梁の断面形と幾何学




林大輔 直前詰め込みベクトル 三角形の面積 三角形の面積は平面の公式と同じ ただしここでは 内積 Cos Sin 面積 を求める手順ができるようにしておこう ベクトルの成分を利用して できて欲しい ことが詰まってます もちろん 面積公式
3.面積ベクトルとは?ベクトルを使った面積の求め方!(演習問題&解説つき) 4.位置ベクトルとは?内分・外分・重心を解説! 5.垂心とは?位置ベクトルを用いて三角形の五心を解説! 6.ベクトル方程式とは?ベクトルの公式を解説! ベクトルの内積と三角形の面積 内積の定義で、 cos cos が出てきましたね。 また、三角比のところで、三角形の面積を表す次のような式を見ました(参考: 基本三角比と三角形の面積 )。 三角比を用いた三角形の面積 ABC A B C の面積 S について、次 面積ベクトルの和 面積ベクトルの重要な性質として,『閉曲面に関して面積ベクトルの総和を取ると零になる』というものがあります.この性質を理解するために,まず平面上の閉曲線 を考えます.曲線を 個の弧に分割し,各分割点の位置ベクトルを とします.そして, と置きます
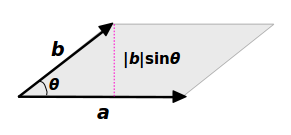



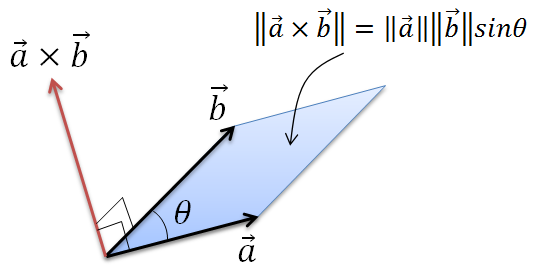
ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ
公式集:ベクトル G ベクトルと図形 G1 ベクトル G11 ベクトルの加法の基本法則 任意のベクトルa, b, c について, ① 交換法則 ab = ba ② 結合法則 (ab)c = a(b c) ③ 零ベクトルの性質 a0 = 0a = a ④ 逆ベクトルの性質 a(−a)=0,(−a)a = 0 G12 ベクトルの平行条件ABjj ACjsin 1 また,ベクトルの内積の公式より証明 はじめに 3次元ベクトル空間の任意のベクトルは、 3つの線形独立なベクトルによる線形結合によって表すことができる (「次元と同じ数だけある線形独立なベクトルは基底になる」を参考) 。 従って、 $0$ でない2つの線形独立なベクトル $\mathbf{a}$, $\mathbf{b}$ とそれらの間の外積
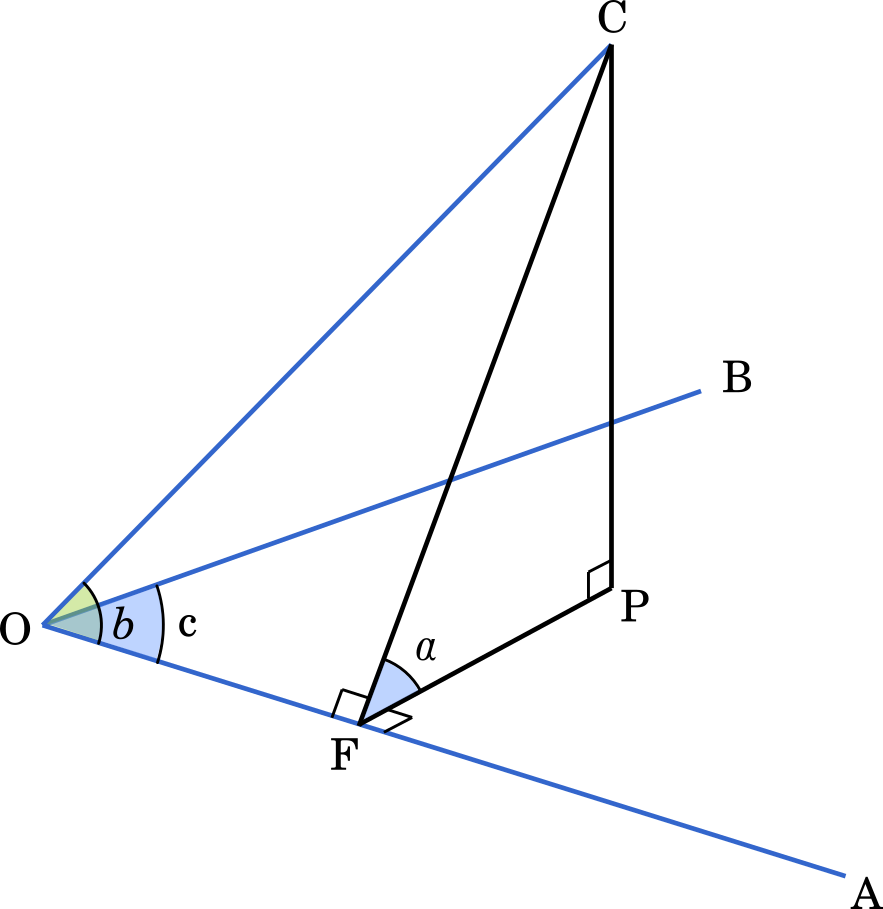



東京都立大18理系第3問 空間ベクトルと四面体の体積の求め方 Mm参考書




倍横距法を用いて多角形の面積を求める方法
ベクトル積の大きさが、ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が作る平行四辺形の面積である、というのはなぜでしょうか。 復習 : ベクトル積について まずは予備知識を復習しておきましょう。 ベクトル積の定義は次の通り。ベクトル関数を面積分するというのは、ベクトルそのものを何か足し合わせていくような操作をするわけではなくて、 法線成分を取り出して作るスカラー量の面積分 (足し算) をする、ということなのです。 d\overrightarrow {S} dS と書いて 面積ベクトル などと平面の法線ベクトル a&b& の長さは、平行四辺形の面積 u S に等しい b & a & S ab && u a,b & が作る平行四辺形を含む面に 垂直で、長さが1のベクトルを法線ベク トルといい、 a b a b S a b




ベクトルを使った三角形の面積公式 Youtube



ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典
ベクトル表示の三角形の面積公式 4 友達にシェアしよう! すべての授業の「要点まとめノート」「問題・解答」をPDF無料ダウンロードできる 学校で使っている教科書にあわせて勉強できる わからないところを質問できる 会員登録をクリックまたは
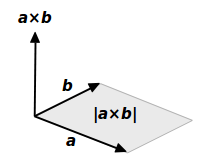



ベクトル積の大きさは平行四辺形の面積 ベクトル解析 基礎からの数学入門
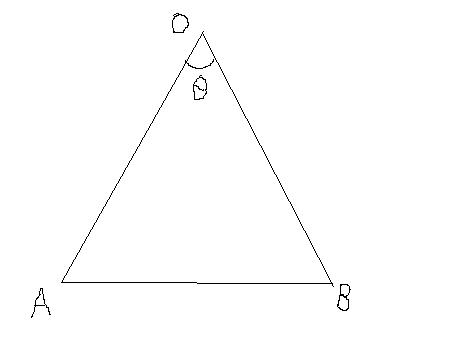



ベクトルでの三角形の面積公式を導く問題です F1 数学 箱根駅伝ブログ




高校数学の ベクトル 内積 三角形の面積公式 に関する問題を解いてみる Yahoo 知恵袋より Makelemonadejp Com



48s96ub7b0z5f Net Bekutoru Menseki



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
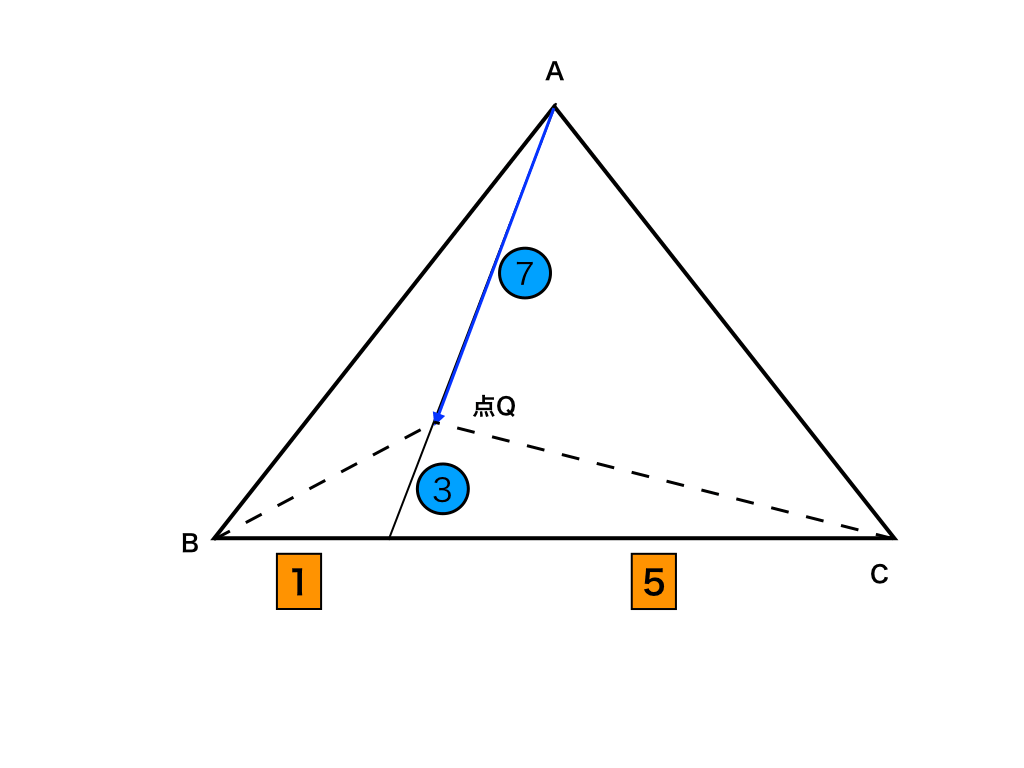



ベクトルの和で表された式から点pの位置を求める方法を解説
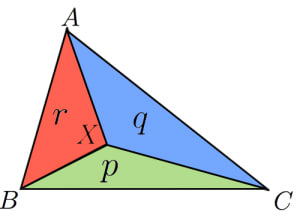



ベクトルの定番問題を一瞬で解く公式 高校数学の美しい物語




ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ




ベクトルの公式一覧 計算 内積 三角形の面積 共線条件 理系ラボ
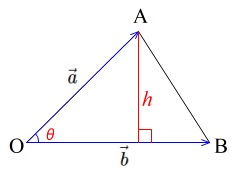



ベクトルの大きさと内積だけで表す面積の公式




平面上の異なる3点を頂点とする三角形の面積 身勝手な主張




平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori



3点からなる三角形の面積を求める イメージングソリューション




重心とは 三角形の重心の座標 位置ベクトルの求め方や公式の証明 面積比の問題を解説 数学 オイラー線 遊ぶ数学



面積ベクトル 物理のかぎしっぽ
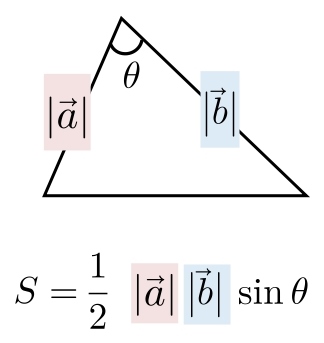



高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト



Www Shinko Keirin Co Jp Keirinkan Kou Math Entrance Pdf 65 Pdf
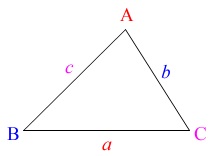



ベクトルの大きさと内積だけで表す面積の公式




ベクトル方程式による面積比の問題と解き方




三角形の面積のベクトル 成分を用いた公式 高校数学の美しい物語




外積とは何か ベクトルの外積の定義 意味 大きさについて アタリマエ




高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト



Studydoctor空間上での三角形の面積 数b Studydoctor



必ず押さえておきたいベクトルの問題その1 Part2 高校数学の知識庫




ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ



空間ベクトルとは 内積 面積などの公式や問題を解くコツ 受験辞典




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




ベクトルの三角形の面積の公式について 高校数学の勉強法 河見賢司のサイト




高校数学b ベクトル表示の三角形の面積公式 映像授業のtry It トライイット




高校 数学b 空間ベクトル11 面積公式 15分 Youtube



48s96ub7b0z5f Net Bekutoru Menseki




ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ
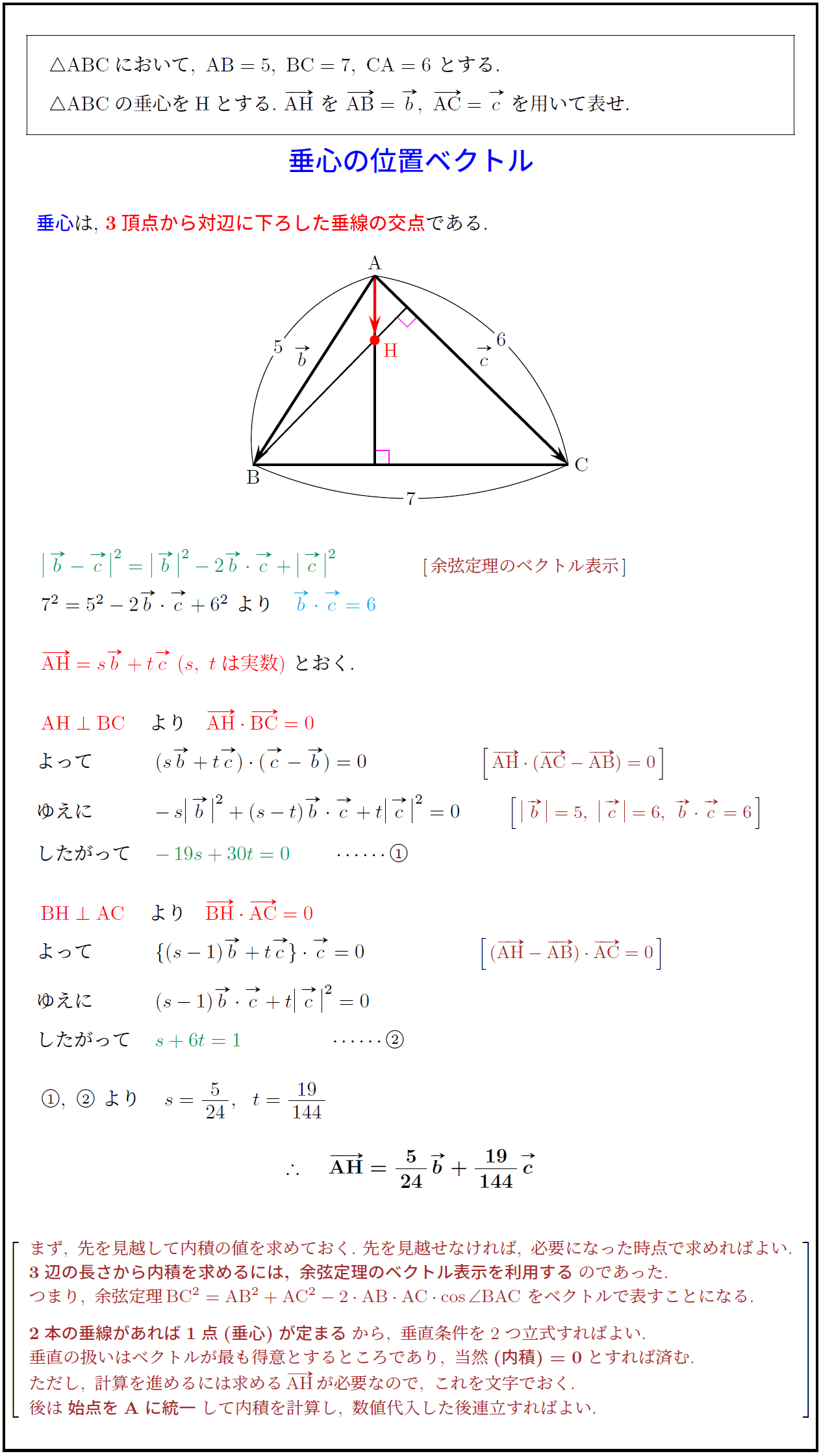



高校数学b 三角形の垂心の位置ベクトル 受験の月




外積を使って解く入試問題例 東大落ちの受験勉強法



48s96ub7b0z5f Net Kuukan Bekutoru Menseki



ベクトルを用いた三角形の面積の公式についてこれは絶対値記号でしょ Yahoo 知恵袋



三角形の面積 ベクトル利用 大学受験の王道




裏技 ベクトルと面積比 これ知らない奴来い Youtube
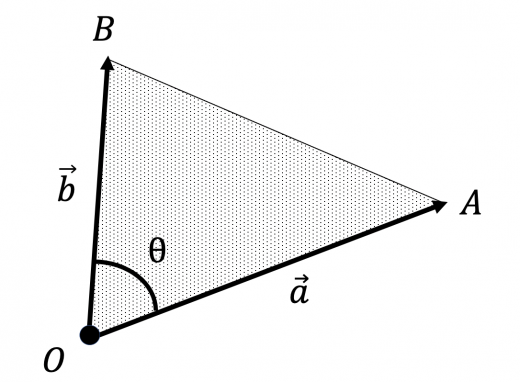



三角形の面積のベクトル 成分を用いた公式 高校数学の美しい物語




ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典



三角形の面積 証明 受験数学って暗記 仮 高校受験 大学受験 楽天ブログ



3




高校数学でよく使う三角形の面積公式まとめ おいしい数学



1




三角形の面積の求め方まとめ 数学の偏差値を上げて合格を目指す




同一直線上にない平面上の3点でできる三角形の面積 ベクトル内積を用いて 高校数学 身勝手な主張



Studydoctor空間ベクトルの成分と演算 数b Studydoctor




三角形の面積の公式 怜悧玲瓏 高校数学を天空から俯瞰する



数学bの内積の三角形の面積の公式の証明についてです 写真で赤線を引っ Yahoo 知恵袋
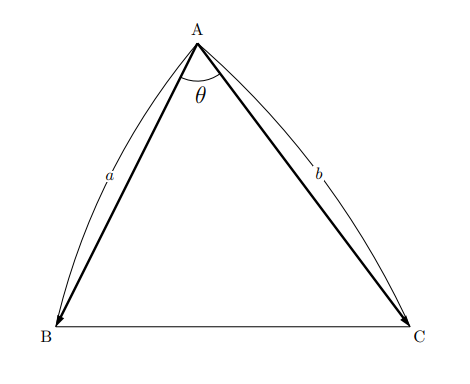



ベクトルにおける三角形の面積の公式の導出とコツ 高校数学の知識庫




高校数学b 空間ベクトルのなす角の計算 映像授業のtry It トライイット




三角形の面積を求める公式7選 高校数学のまとめにどうぞ



Studydoctorベクトルと三角形の面積公式 数b Studydoctor




ベクトルを用いた三角形 平行四辺形の面積の公式と求め方 高校生向け受験応援メディア 受験のミカタ
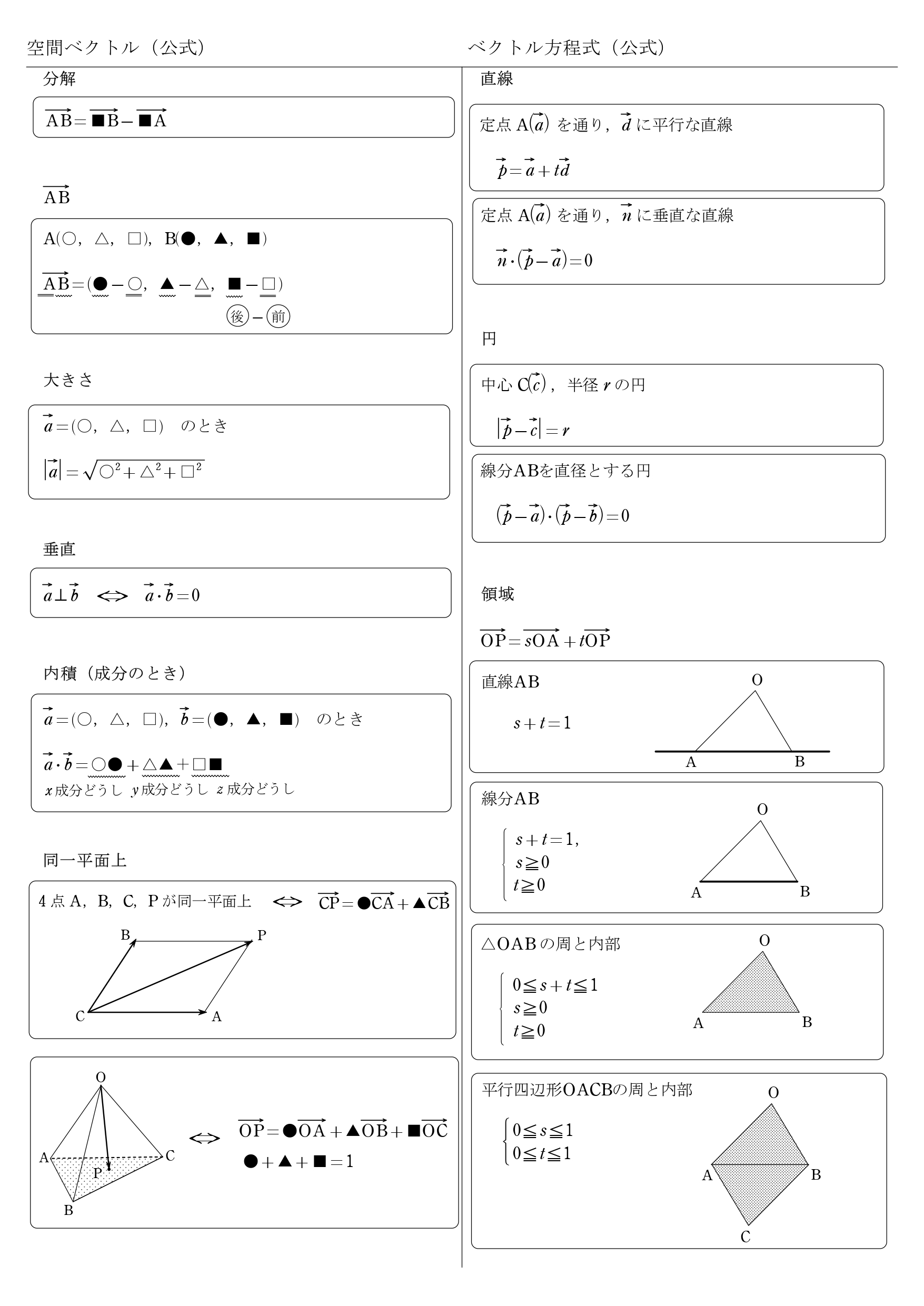



高校数学b 空間ベクトル 公式一覧 4点が同一平面上 学校よりわかりやすいサイト




高校数学b ベクトル表示の三角形の面積公式 練習編 映像授業のtry It トライイット



空間ベクトルその他立体問題 京極一樹の数学塾




ベクトルを用いた 三角形の面積の公式 数学b By Okボーイ マナペディア



四面体の体積



外心の位置ベクトルについて質問です ベクトルの面積比の Yahoo 知恵袋



48s96ub7b0z5f Net Kuukan Bekutoru Menseki



数bベクトル ベクトルで作る三角形の面積を導出する Mm参考書




外積を使って解く入試問題例 東大落ちの受験勉強法
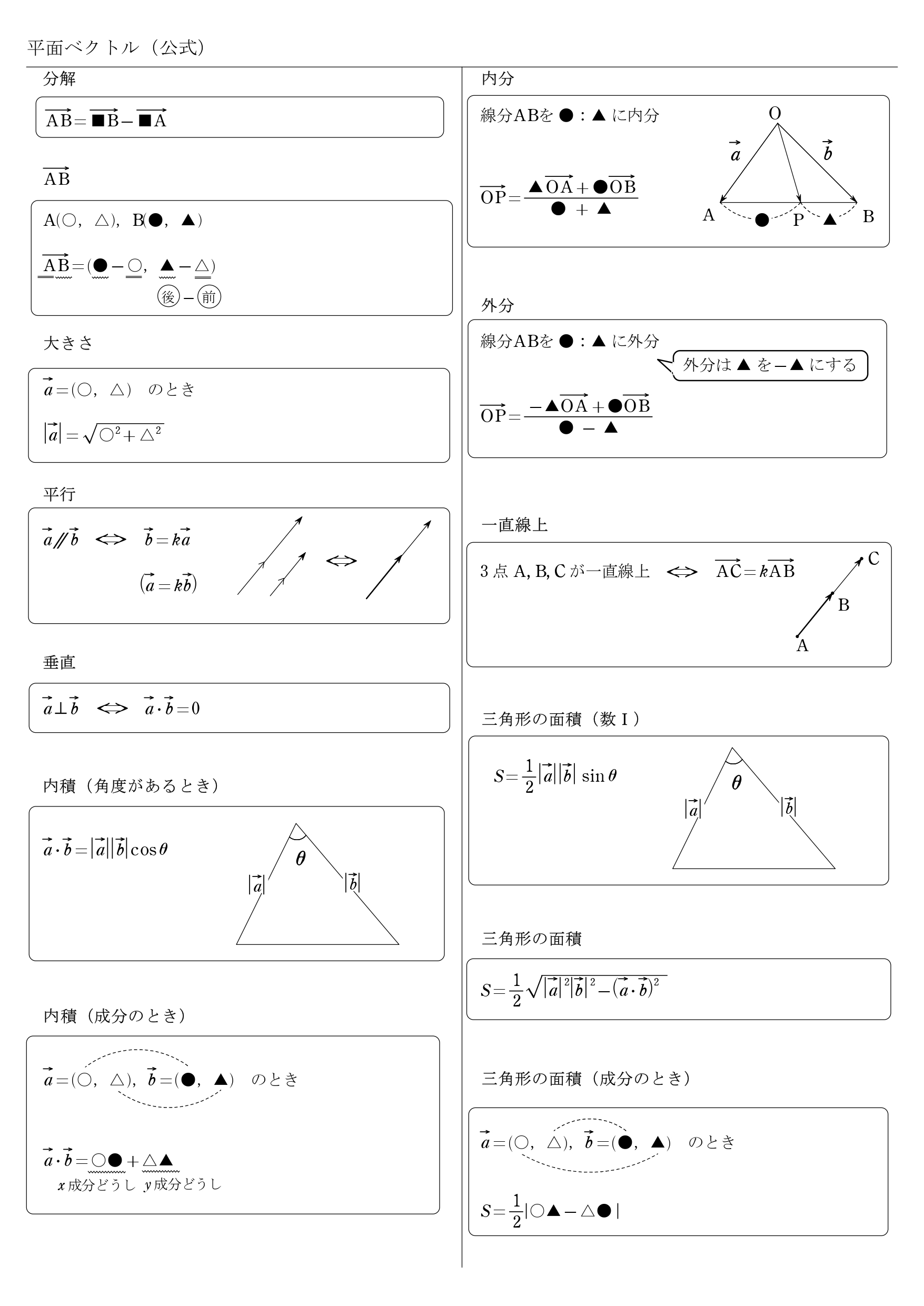



高校数学b 平面ベクトル 公式一覧 内分 外分 面積 学校よりわかりやすいサイト



Q Tbn And9gct71t318twmynw63dxmqoj5dsomuiz6o0rnzjk6hursgayaq9 L Usqp Cau
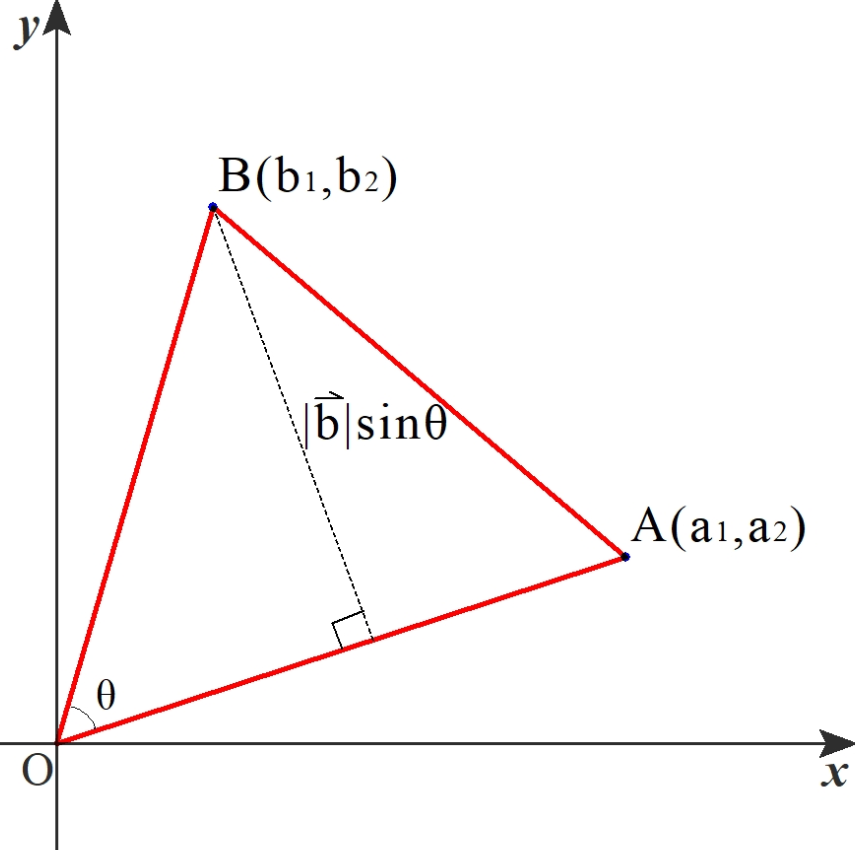



ベクトルを用いた三角形の面積公式3種類 数学の庭




基本 空間上での三角形の面積 空間ベクトル3 06 Youtube




高校数学b ベクトル表示の三角形の面積公式 映像授業のtry It トライイット



外積を利用した2つのベクトルに垂直なベクトルの求め方とは 大学入試数学の考え方と解法



ねこ騙し数学




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学




高校数学b 三角形の面積のベクトル表示 成分表示とその証明 受験の月




勉強しよう数学 三角形の高さベクトルhの公式



大学入試に必要な三角形の面積について 楽しく学ぶ大学受験数学




この三角形の面積公式はなぜこうなるのですか Clear




ベクトルでの三角形の面積公式を導く問題です F1 数学 箱根駅伝ブログ




高校数学でよく使う三角形の面積公式まとめ おいしい数学
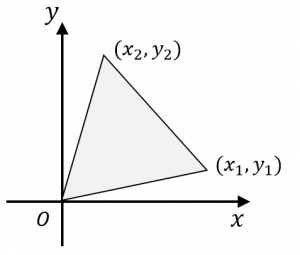



座標平面上で三角形の面積を計算する公式 具体例で学ぶ数学




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学




新訂版序文の人 大類昌俊 外出連続50日目 高校数学の参考書を読めば道具のように使われているのが分かるし 高校数学bで平行四辺形の面積の公式 検定教科書では必須ではないが非常に便利 または大学数学でベクトル空間 空間ベクトル を学ぶ時の初等的な




勉強しよう数学 三角形の3頂点のベクトルの張る三角形の面積比の公式




ベクトルの外積と平行四辺形の面積 身勝手な主張




ベクトルによる三角形の面積公式 ゼロからわかるベクトル第13回 Youtube



ベクトルによる三角形の面積の求め方 公式や証明 計算問題 受験辞典
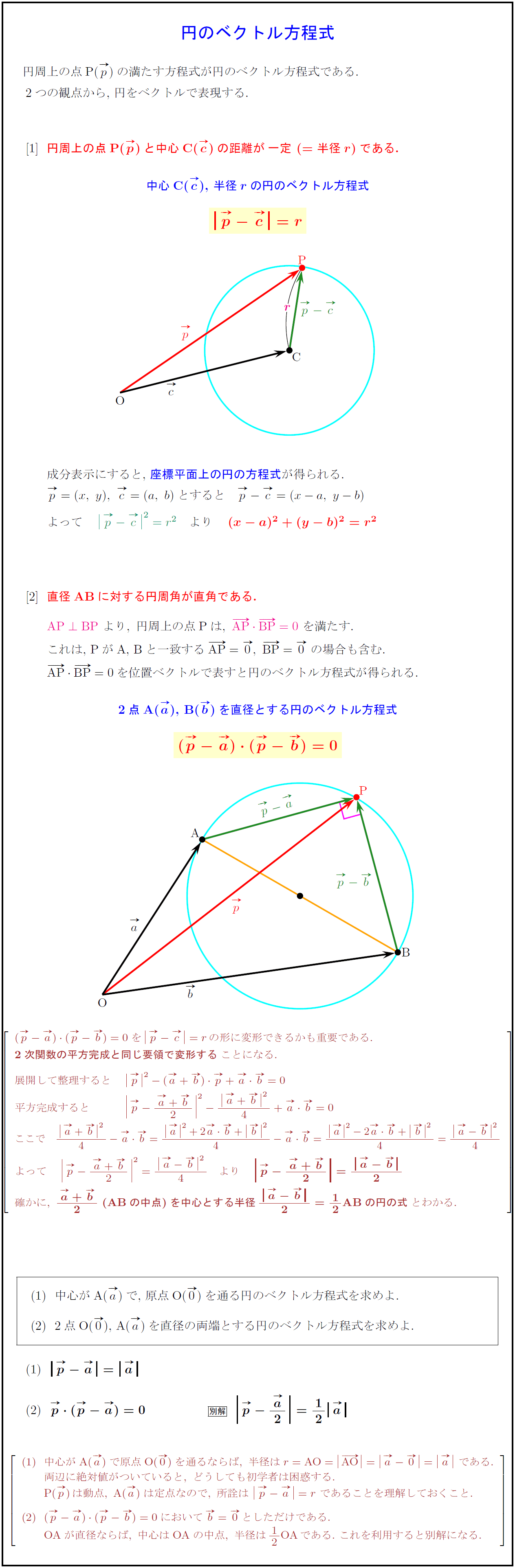



高校数学b 円のベクトル方程式2パターン 受験の月
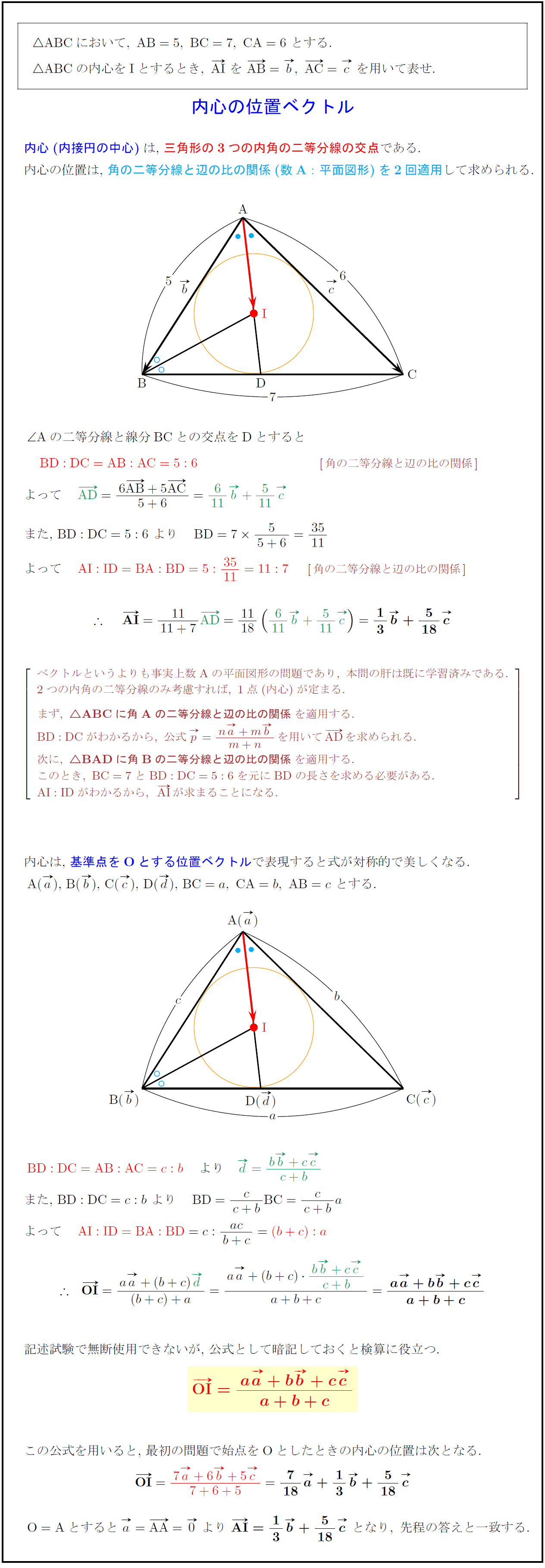



高校数学b 三角形の内心の位置ベクトル 受験の月




ベクトルの三角形の面積公式を超わかりやすく説明した 理系ラボ



48s96ub7b0z5f Net Bekutoru Menseki




三角形の面積の求め方とは Sinやベクトルを用いる公式も解説 小学生から高校生まで 遊ぶ数学



0 件のコメント:
コメントを投稿