6/4/ ここでは整数を並べてできる3の倍数の個数を求める問題について説明します。 まず,3の倍数の見分け方を知っておこう。 3の倍数 各位の数字の和が3の倍数のとき,元の数は3の倍数である。 数学IA順列に関する問題の考え方 ここでは「順列」について説明します。順列とは,いくつかあるものを順序をつけて1列に並べる配列のことです。意味を考えて17/6/19 高校数学A 場合の数 集合の要素の個数(個数定理) 和の法則と積の法則、樹形図・表の作成による数え上げ;中学受験 5年 unit 71 場合の数1 順列と組み合わせ1 3の倍数条件は絶対に覚えておきましょう。 ご利用頂きまして誠にありがとうございます。 ご記入頂いた内容は完全に非公開です。 みんなの算数オンラインはユーザーの皆様からのすべての

数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法
場合の数 順列 倍数
場合の数 順列 倍数-12/4/ ここでは同じものを繰り返し使っても良い場合の順列について説明します。 例えば1, 2, 3の3つの数字を使ってできる整数を考えると,3桁の整数を作る場合であっても,1回しか使えない場合より多くの整数を作ることができるようになります。 実際,百の位・十の位・一の位の数字の選び方はそれぞれ1, 2, 3の3通りあるから, 3 3 = 27 個の整数を作ることができ この中に5の倍数は(1)より21個ありましたね。 つまり、5の倍数でない整数は $$=80個$$ となります。 「~でない」という場合には、全体の個数から「~である」を引いてあげれ




数a 場合の数 積が4の倍数になる Youtube
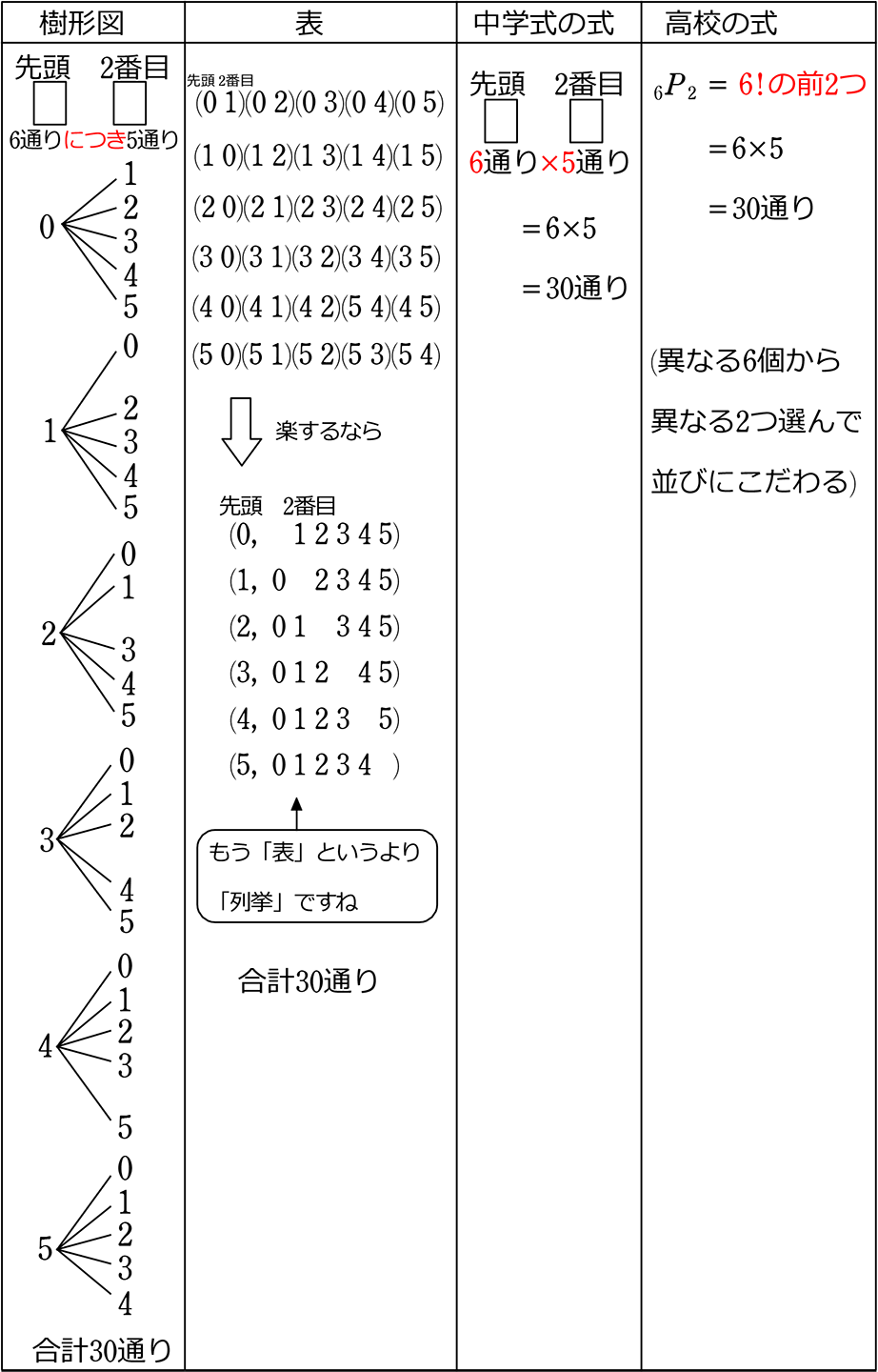
19/5/21 場合の数・順列・倍数算数・数学う山先生の挑戦状う山TV(スタディ) ────────────────── 算太・数子の算数教室(r) 算数合格トラの巻 う山TV(スタディ) う山TV(バラエティ) カンブリア・アカデミー ────────────────数学A advance 1章「場合の数と確率」 3 0 以下の自然数のうち,次のような数の個数を求めよ。 (1) 6 でも 8 でも割り切れない数 (2) 6 の倍数であるが,8 の倍数ではない数 0 以下の自然数全体の集合をUとする。 この2種類の問題では、それぞれ答えが変わってきます。 ①は順列で、答えは 5 p 2 =5×4=通り ②は組み合わせで、答えは 5 c 2 =5×4÷2=10通りになります。 今回は、そんな順列と組み合わせの数の考え方についてです。
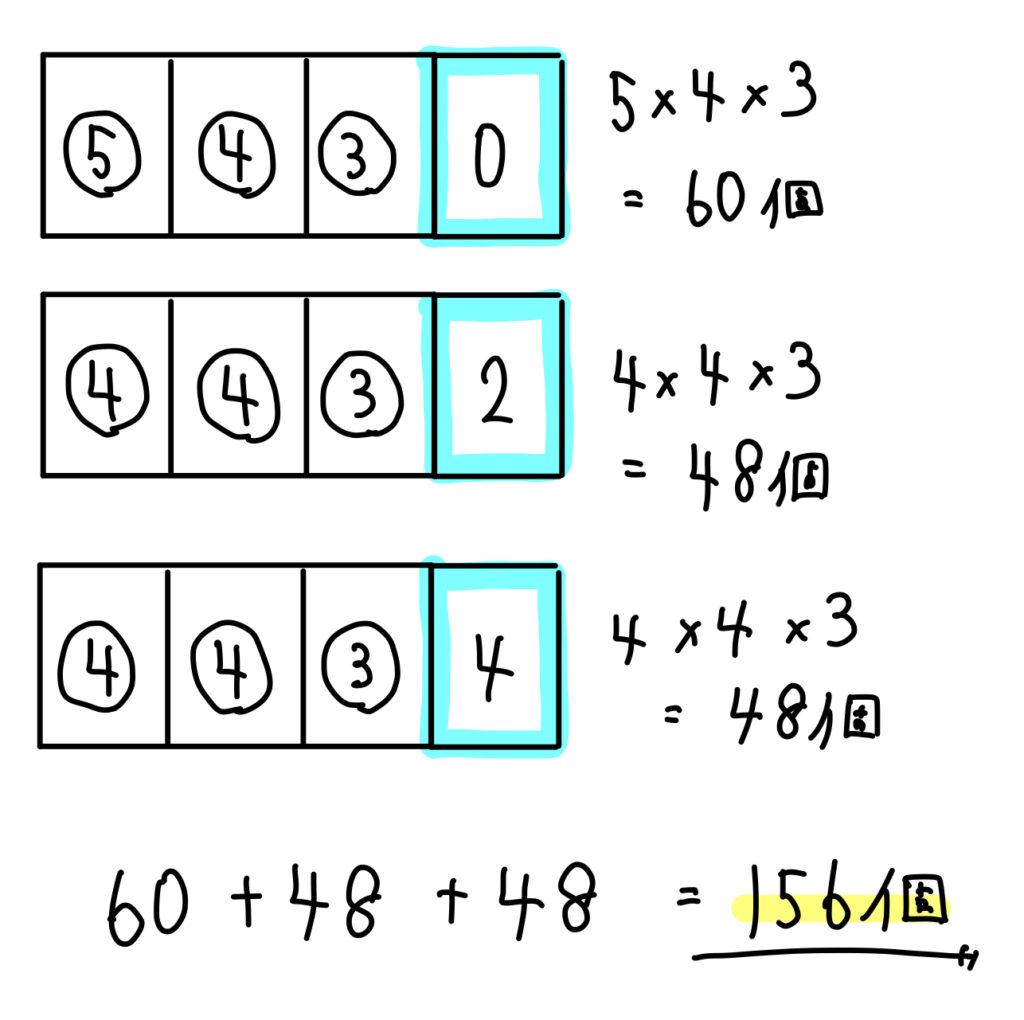
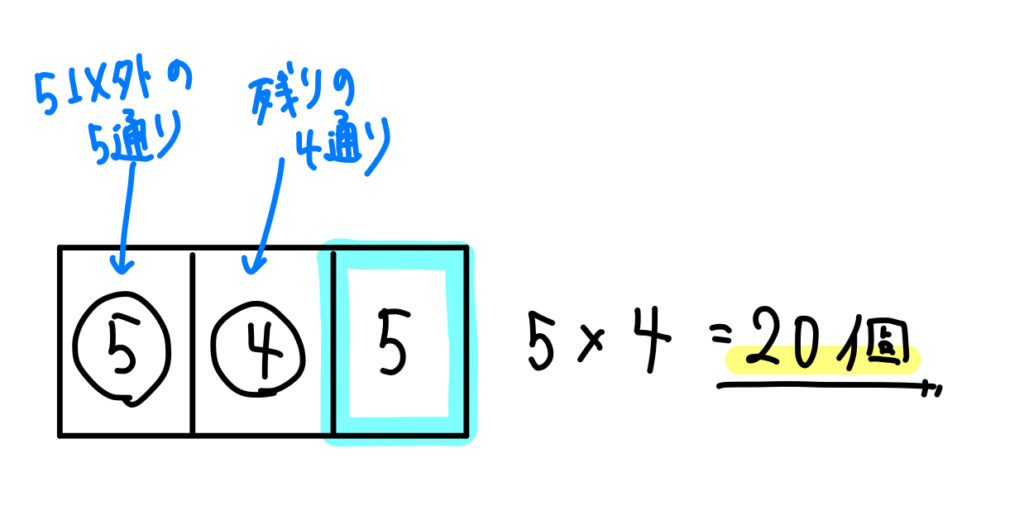
(2) 1の位の数は5 1通り その各々について,残りの桁の決め方は 5・4・3=60通り ゆえに,60通り・・・(答) (3) 1,2,3,4,5,6から4個選んで和が3の倍数となる組合せは ア) 1,2,3,6・・・和は12 イ) 1,2,4,5・・・和は125/9/19 千、百、十の位は残りの8個から3個とった順列 8 p 3 よって8× 8 p 3 =8×8・7・6=26 1,2より5桁の5の倍数は=5712 個 (2) 千の位が1になる整数は 5 p 3 個ある。 千の位が2,3,4,6の場合も同様に 5 p 3 個ずつある。偶数になるのは、一の位の数が0か2の場合。 一の位の数が0のとき、十の位の数は1、2、3の3通り。 一の位の数が2のとき、十の位の数は1、3の2通りなので、全部で5通り。 (3) 4の倍数は12、、32の3
1/5/ 一の位が奇数数\((1,3,5,7,9)\) 3の倍数 各位の数の和が3の倍数 4の倍数 下2桁が4の倍数 5の倍数 一の位が0または5 6の倍数 2の倍数 かつ 3の倍数 (各位の和が3の倍数であり,一の位が偶数) 9の倍数 各位の数の和が9の倍数席が4桁で、要素の数が1~6の6個なので、 「要素の一部を並べる」問題だとわかるね。 ここまでで、この問題は、「全て異なる(n個の)要素のうち一部(r個)を使って、 直線の席に当てはめる問題」と見分けることができた。 この問題は、 順列の記号 n P r をそのまま使うことができるよ。 1~6の6個から異なる4個を使って並べ替えるので、 6 P 4 = 6!センター試験(類題)整数と順列のポイントは! ・4 の倍数の条件は、下2桁が 4 の倍数になること! ・5の倍数の条件は、一の位が0か5になる




第1章 場合の数と確率 第1節 場合の数 3 順列 第3回 Ppt Download




順列の問題 一定の条件で並べる 高校数学の知識庫
日本大百科全書(ニッポニカ) 順列・組合せの用語解説 n個の異なるものからr個を取り出して1列に並べたものをn個からr個とる順列といい、その総数をnPrと書く(Pは、順列の英語permutationの頭文字をとったもの)。たとえば、4個の文字A、B、C、Dから3個をとって並べると、次のような24通り19/5/21 場合の数・順列・倍数算数・数学う山先生の挑戦状う山TV(スタディ) ────────────────── 算太・数子の算数教室(r) 算数合格トラの巻 う山TV(スタディ) う山TV(バラエティ) カンブリア・アカデミー ────────────────15年度 中学入試に向けて 3 Tweet 場合の数の練習問題 | 14年04月12日18時00分 第177回 「場合の数 3」 明治大学付属明治中(日能研 14年度入試結果R4偏差値60) 平成26年度用 中学校別入試問題シリーズ(東京学参) 今回は「場合の数」の苦手克服の第3回




組み合わせの総数 場合の数 理数系無料オンライン学習 Kori




順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ
場合の数・順列・倍数算数・数学う山先生の挑戦状う山TV(スタディ) ────────────────── 算太・数子の算数教室(r) 算数合格トラの巻 う山TV(スタディ) う山TV(バラエティ) カンブリア・アカデミー ────────────────つまり、順列の問題とは、 「 n個の要素を、r個の異なる席に当てはめる場合の数 」を求める問題、と言えます。 基礎的な問題では、「要素の並べ替え」でも「席に当てはめ」でも ほとんど変わらないように思えるかもしれませんが、2 場合の数・順列─11 ポ イン ト ① 〔積の法則〕2つのことがらA,Bが あ って ,Aの 起こ り 方が m通りあり,そのおのおのに対し て,Bの起こ り 方 が n通りあるとき ,Aと Bがともに起こる 場 合の数は mn 通りである. ② 積の法則は,AかつBが 起こるとい う 2つ の場 合 だけでなく ,AとBとCが



3




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々
100÷3 を計算します。 100÷3= 33・・・1 (100 = 3×331) 商は、「33」となることから、 「33個」と分かります。 これを、集合の要素の形で表すと、解答解説のように A= { 3∙1 , 3∙2 , 3∙3 ,・・・, 3∙33 } と表せるわけです。 次に ≪ (2)「5の倍数でない整数」 を求める問題≫ 1, 2, 3, 4, 6, 7, 8, 9, 11,・・・・などと、5の倍数ではないものを、考えると数が多くて、数えるの19/5/21 このとき「12の倍数」は何通り作れますか? 算数・数学・う山先生の挑戦状 場合の数・順列・倍数 ────────────────── (o^')b う山先生の挑戦状です♪ 君は解けるかな? 中学受験、高校受験、大学受験、そして「2の倍数 または 3の倍数」というのは、 (2の倍数)∪(3の倍数) ということ。 つまり、 「2の倍数と3の倍数の和集合」 だよ。 「かつ」 とか 「または」 という表現が出てきた瞬間に、この集合のイメージを思い浮かべられるようにしよう。




02 03n桁の倍数の数字を作る順列 難易度2




教科書レベルの問題一覧と解答 数学a 場合の数と確率 教科書より詳しい高校数学
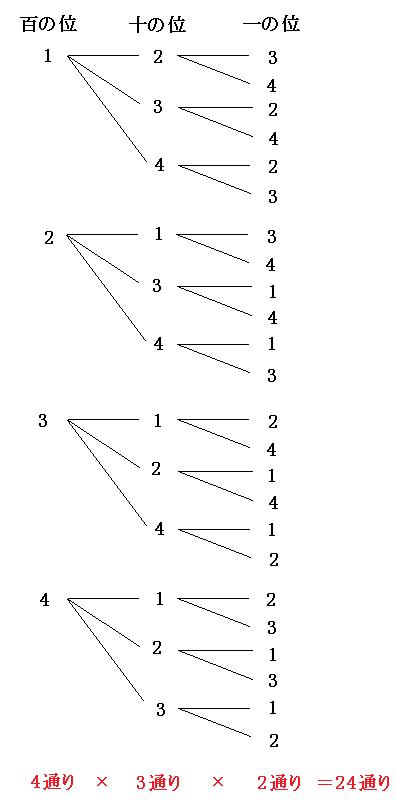
2/3/16 与えられた整数を並べて、3の倍数や9の倍数が何通りつくれるかを求める問題です。 3の倍数:各位の数の和が3の倍数になります。 9の倍数:各位の数の和が9の倍数になります。 まず数の選び方を考え、次に並べ方を求めます。 0が含まれる場合と含ま5.集合,場合の数 1から1(xoまでの自然数のうち,6の倍数であって4の倍数でないものの個数は口である。 (北海道工大) (1)1から9までの9個の数字から異なる3つの数字をとって3桁の数をつくるとき,それが偶数と なるのは全部で⊂コ通りである。あることがらについて、その起こり方が何通りあるか調べることを、場合の数を求めるといいます。 順列 いくつかのものを順番に並べるときの並べ方を順列といいます。 順列の場合の数の求め方 順列の場合の数の求め方には、計算で求める方法や、樹形図をかく方法などがあります。 abcの順にかくなど、ルールを決めてかくと、 樹形図のかき方




高校数学a 倍数の個数1 かつ または 例題編 映像授業のtry It トライイット




順列の問題なのですが式がどうして 写真のような式になるのかわかりません その理由を Clear
3の倍数には面白い性質があります。 ・3の倍数の全てのケタの数を足し合わせると、それも3の倍数になる。 (例 1362は、全てのケタの数字を足すと 1 3 6 2 = 12 で3の倍数。 1362 = 3 × 454 なので、確かに1362は3の倍数。 ) この性質は主に素因数分解場合の数・順列(4) 名前 1a,b,c,d,eの5人で班をつくります。 (1) 班長、副班長を1人ずつ決めるときの場合の数は何通りですか。 式 答え (2) aを先頭に5人で並ぶときの場合の数は何通りですか。 式 答え (3) 5人で1列に並ぶ場合の数は何通りですか。 式 答え中学受験 4年 unit 423 場合の数4 倍数の作り方 例題と解説 トレーニング 確認テスト ログインが必要です 関連する過去問 4年生向け 市川中学校06 場合の数




解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




高校数学a 各位の大小関係が決められた整数の順列 A Gt B Gt C Gt Dなど 受験の月
(iv) 5の倍数を得るためには最後の数が0か5であればよい。 このとき最後が0になる場合の数は他の4つが任意であるため !倍数の条件のポイントは!・2の倍数の条件は, 1の位が0を含めた偶数・3の倍数の条件は,各位の和が3の倍数・4の倍数の条件は,下2桁が 4 の倍数・5・偶数は、一の位が 0 のときと, 0 以外の偶数のときに場合分けしよう! ・奇数は、全体の個数から偶数の個数を引こう! ・3 の倍数は,和が 3 の




高校数学 数a 10 順列 数字編 Youtube




場合の数 順列 P と組合せ C の違いは どう使い分ける ますますmathが好きになる 魔法の数学ノート
今回から 「順列」の場合の数 について学習しよう。 「順列」とは、漢字が表す通り 「順番をつけて並べる」 ということ。順番をつけて並べる場合の数 は、とても重要なテーマで、様々なパターンの問題があるんだ。 これから計10回にわたって、順列の問題のパターン別解法を説明していくよ。( 6 4)!確率 順列 4桁の5の倍数 0からのセンター試験数学 今回は5の倍数です。 『0、1、2、3、4、5の数字を一回だけ使えるとき』(3)4桁の5の倍数の数5の倍数は一の位が0か5なので、場合分けしていきます。 (i)一の位が0のとき残りの5個の数字から3個選んで千、百、十の位に割り当てます。 よって5P3となります。 (ii)一の位が5のとき千の位4通り百と十の位4P2よって4



数学 順列 1 2 3 4 5の5個の数字を1個ずつ Yahoo 知恵袋




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん
5/9/19 集合の要素の個数 場合の数 順列 円順列・重複順列 組合せ 同じものを含む順列、重複組合せ 確率 確率の基本性質 独立な試行 反復試行 図形の性質 三角形の辺の比 三角形の五心 チェバの定理、メネラウスの定理 円に内接する四角形 円と直線 方べきの定理 2つの円



場合の数 学び家 Com




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



順列9の倍数になるとき次のような問題で 和が9とか3になるよう Yahoo 知恵袋




1 P6 1 1 4 2 Descubre Como Resolverlo En Qanda




3 は 2 の答えを利用して解く問題なのですが Clear




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら



数学 順列 1 2 3 4 5の5個の数字を1個ずつ Yahoo 知恵袋




高校数学 数a 勉強動画 順列 数字編の問題 19ch




場合の数 円順列 じゅず順列 重複順列 22中学受験 検 指南




数探高校講座 数学a 場合の数と確率 3 順列 数学探究所




場合の数と確率 倍数の個数の求め方 数学a 定期テスト対策サイト




高校数学a 倍数の個数1 かつ または 練習編 映像授業のtry It トライイット



場合の数 順列と組み合わせの違いと並べ方問題の解き方




場合の数17 数の順列1 怜悧玲瓏 高校数学を天空から俯瞰する




場合の数 順列と組合せ Spi3非言語対策 よりくわ先生 Note




順列 異なるものを並べる場合の数は樹形図や積の法則で求めよう みみずく戦略室




高校数学a 数字の順列 4桁の奇数 偶数 倍数の個数 受験の月



同じものを含む順列の問題です 0が存在する数字の問題は 先頭に0がくるもの Yahoo 知恵袋



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ



1



Happylilac Net Baainokazu Ans Pdf



順列の問題です 0 1 2 3 4 5の数字を用いて4ケタの整数を作ると Yahoo 知恵袋



場合の数の公式 応用 円順列 重複順列 重複組み合わせ等 そうちゃ S 図解英数ゼミナール




重複順列とは 基本公式と解き方を解説 高校生向け受験応援メディア 受験のミカタ




中学受験 算数確認チェック29 場合の数 順列 組み合わせ グランパは元塾長




場合の数18 数の順列2 怜悧玲瓏 高校数学を天空から俯瞰する



2



数学の問題です 次の順列の総数を求めよ 1 4人の生徒を1列に並べる順 Yahoo 知恵袋



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




整数と順列 超わかる 高校数学 A 授業 場合の数 8 Youtube



中学数学 場合の数



場合の数の一般問題 京極一樹の数学塾




順列と組み合わせの違いとは そしてそれぞれの意味を0から解説



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



Q Tbn And9gcsj032wcr 6cnslcx5wupxgh7s0hmxa00qycwq7lsonp0ubhpos Usqp Cau




場合の数 順列 組合せ のブログ記事一覧 知能問題 数的処理 判断推理 数的推理 数学パズル spi 空間把握 解いてみてください




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々




数a 場合の数 積が4の倍数になる Youtube




4の倍数 8の倍数になるような数字とは 例えばなんですか Clear




基本問題 場合の数3 順列 0を含む順列と倍数 No Youtube



必修 4 4 異なる要素の順列 席に制限がある順列 わかりmath




場合の数 円順列 じゅず順列の違いと同じものを含む円順列を解説します




場合の数 順列は2時間で解けるようになる 外資系コンサルタントが主夫になったら




高校数学a 倍数の個数1 かつ または 例題編 映像授業のtry It トライイット




数の順列2 怜悧玲瓏 高校数学を天空から俯瞰する



両端指定 整数の順列



数学ia 重複順列の場合の数の求め方 大学入試数学の考え方と解法




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




の倍数は何通りできるか問題 数学の偏差値を上げて合格を目指す




3分でわかる 確率の問題を解くための6つの基礎知識 合格サプリ




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々




センター試験 類題 整数と順列 超わかる 高校数学 A 演習 場合の数 9 Youtube



必修 4 4 異なる要素の順列 席に制限がある順列 わかりmath




順列 数学a フリー教材開発コミュニティ Ftext




3講 順列 1章 場合の数と確率 問題集 高校数学a




知らないと受験で損をする 倍数の見分け方とその使い道



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ



Q Tbn And9gcsoruuip8biibmmwkloy6wj7wk Yjy6la57rlyf3sbz2kbusuws Usqp Cau




場合の数 大中小3つのサイコロを投げるとき何通り 奇数 偶数 4の倍数 数スタ




場合の数 同じものを含む順列について 日々是鍛錬 ひびこれたんれん




15年10月 怜悧玲瓏 高校数学を天空から俯瞰する



Bkro3ef61vmrwm




数学ia 整数を並べてできる3の倍数の個数を楽に求める方法 大学入試数学の考え方と解法
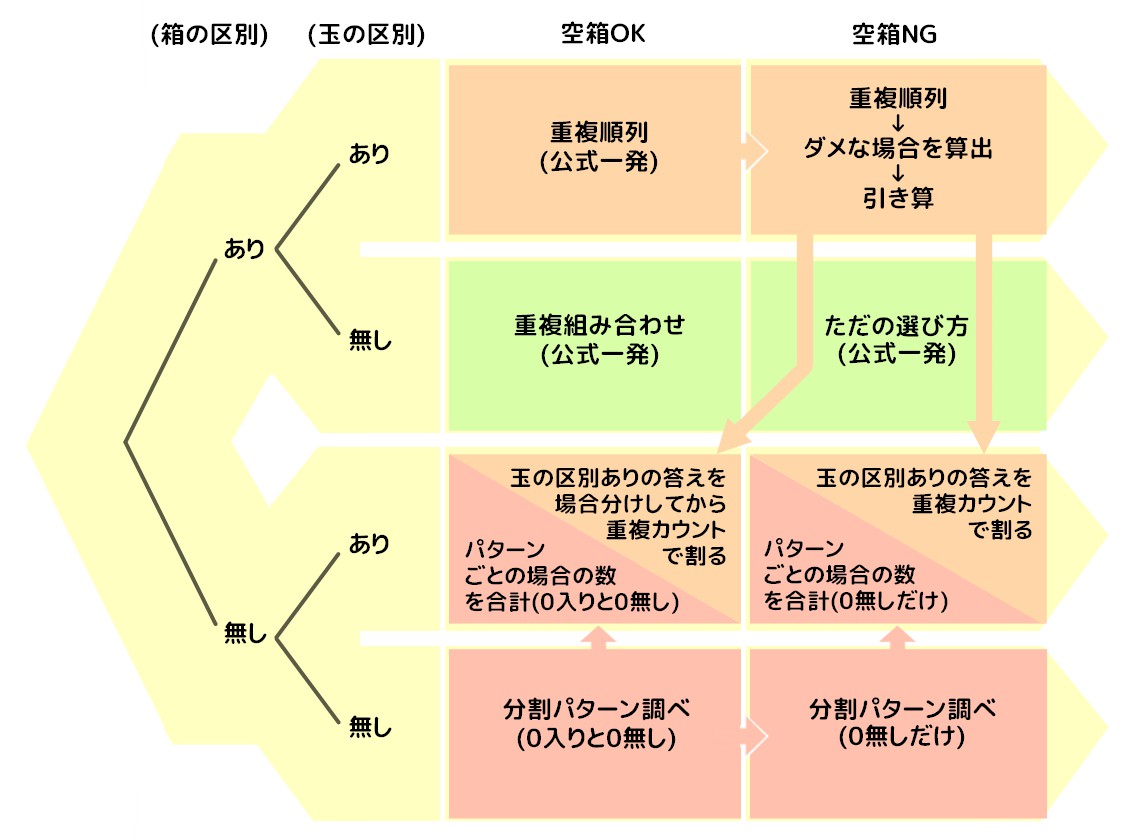



場合の数 確率の総合案内 定理 公式の総まとめと復習 そうちゃ S 図解英数ゼミナール
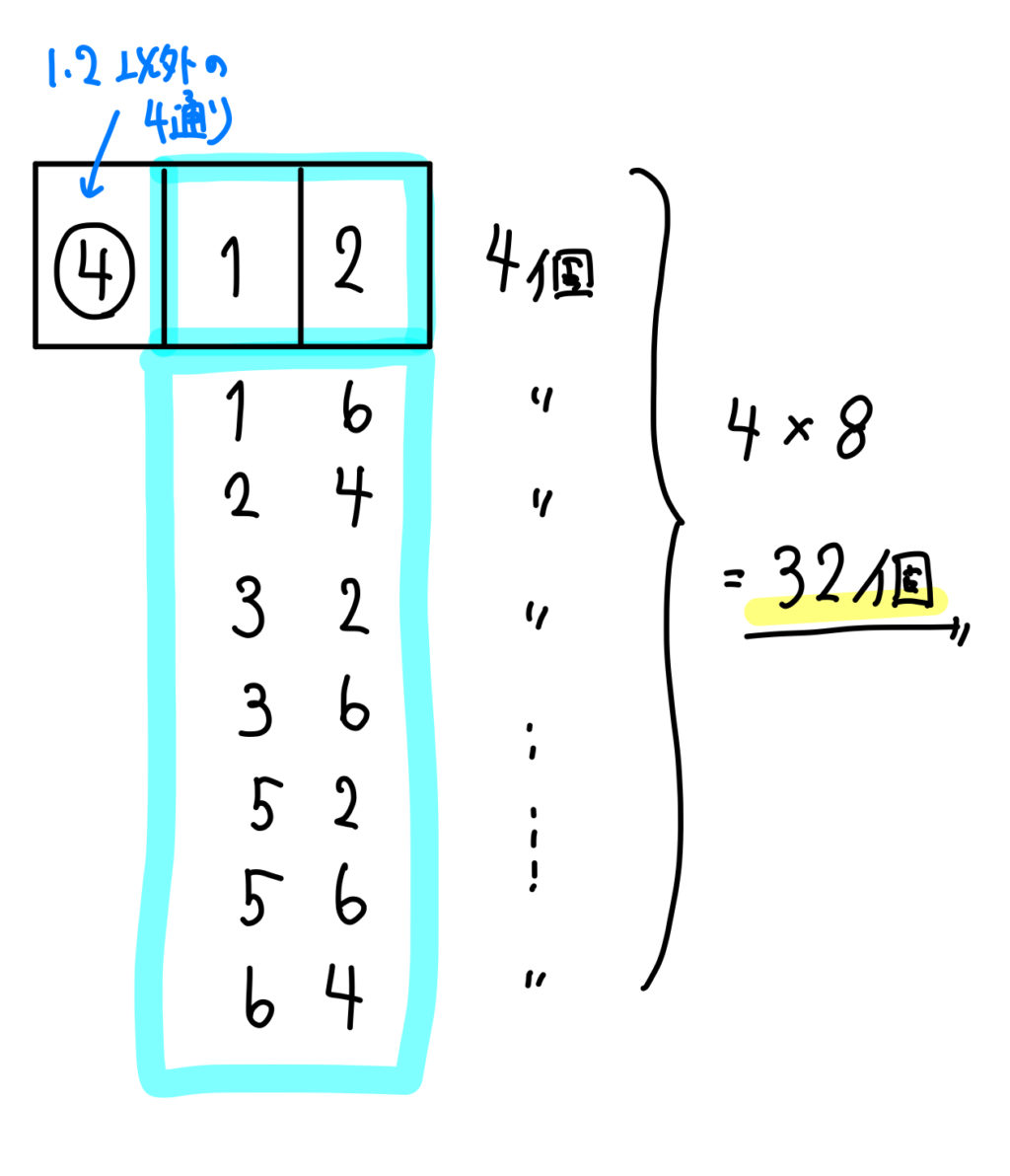



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ




場合の数の勉強方法 組み合わせと順列の解き方と勉強のコツ



場合の数の問題で 3の倍数 の数え方 例題 1 5の数字が書かれた5枚の Yahoo 知恵袋




第1章 場合の数と確率 第1節 場合の数 3 順列 第3回 Ppt Download




3講 順列 1章 場合の数と確率 問題集 高校数学a



Http Toitemita Sakura Ne Jp Standard 12ab 18 18 16 Pdf




中学数学 場合の数



場合の数の一般問題 京極一樹の数学塾
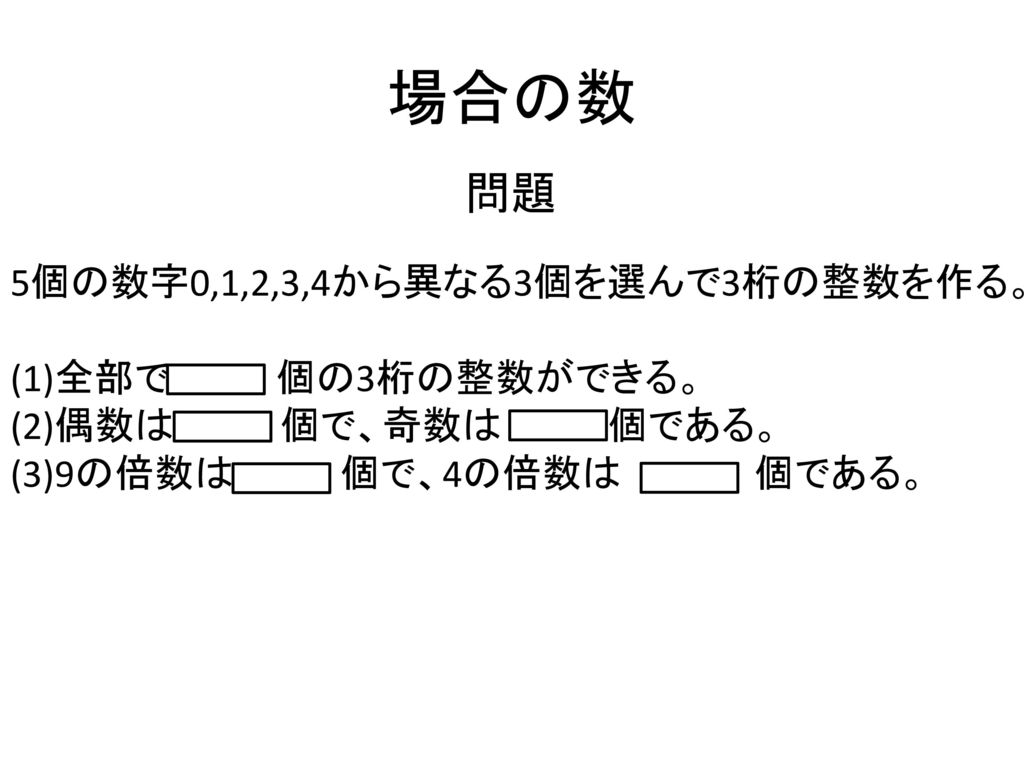



5個の数字0 1 2 3 4から異なる3個を選んで3桁の整数を作る Ppt Download



数学i Aチェック リピート 第7章 2順列 組合せ 1 重複順列 順列 Pukiwiki




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ




場合の数の数え方 P C P H 感じる科学 味わう数学



数学aの順列 組み合わせについて教えて下さい 1 2 Yahoo 知恵袋




数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法




センター試験 類題 整数と順列 超わかる 高校数学 A 演習 場合の数 9 Youtube




順列の問題なのですが式がどうして 写真のような式になるのかわかりません その理由を Clear




の各位の和が3の倍数になる組って地道に考えるしかないのでしょうか Clear




場合の数 順列 倍数 算数 数学 う山先生の挑戦状 う山tv スタディ う山tv エキサイトブログ



必修 4 4 異なる要素の順列 席に制限がある順列 わかりmath




3の倍数 9の倍数は各位の和だと聞いたので 1個ずつ書き出してみたのですが これでは Clear



0 件のコメント:
コメントを投稿