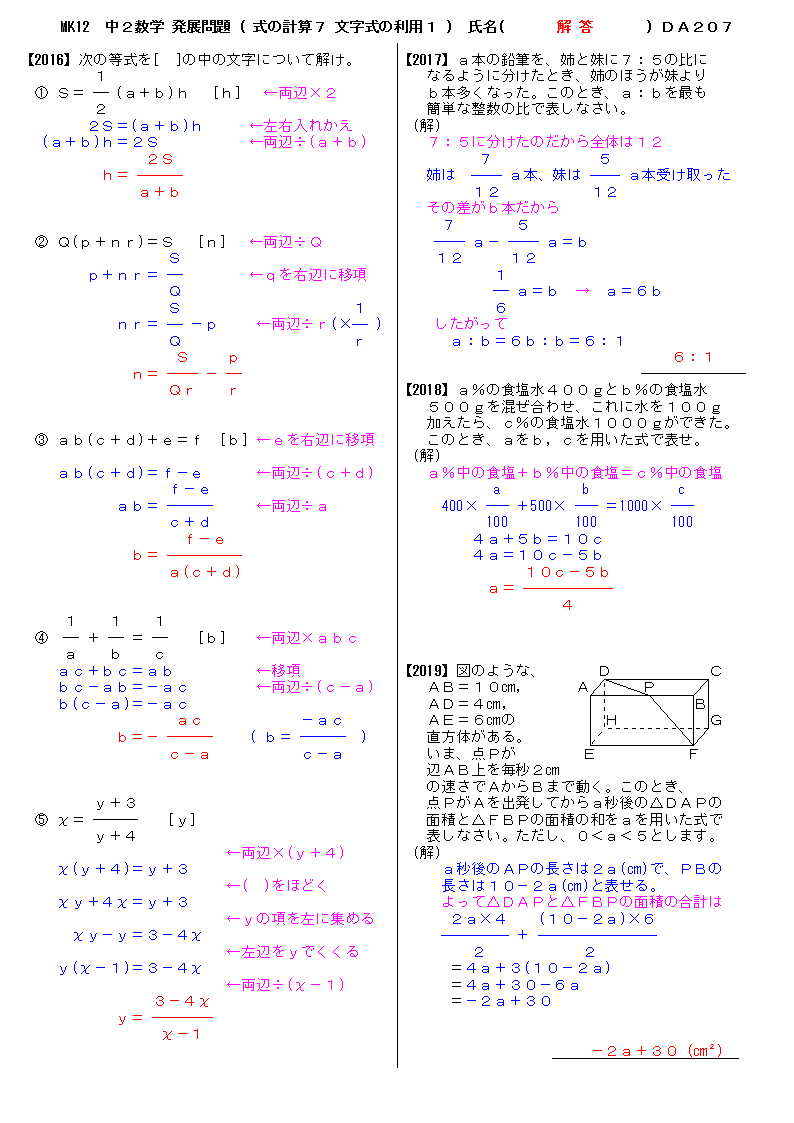
面積公式から分かること 角を1つ共有する2つの三角形の面積比は，その角を作る2辺の長さの積の比に等しいことが分かります。つまり，図において， a b c abc a bc a d e = a b ⋅ a c a d ⋅ a e ade=ab\cdot acad\cdot ae a d e = a b ⋅ a c a d ⋅ a e が成立します。X=3 或4 若 ab =3，則 bc =7−3=4；若 =4，則 =7−4=3。 所以矩形abcd 長若是4、寬會是3，面積=3×4=12。 第四個要介紹的是正方形，四邊會等長而且四個內角都是 直角的四邊形就是「正方形」。 因為正方形的四邊會等長，所以正方形就是菱形的一種；又因為正方三角形の面積だけ求めれば良いのなら，3つの頂点の座標から面積を求めることもできる。 別の考え方と解答 上の計算から，3つの頂点の座標はA$(4,~6)$，B$\left(\dfrac{6}{5},~\dfrac{16}{5}\right)$，C$(6,~0)$ と分かる。
三角形的面積
これは,\ {「2つのベクトルa,\ bが平行ならば面積は0になる」}という当たり前のことを意味する 高校数学で最も鬱陶しい公式の1つだが,\ 以下の三角形の面積の公式は要暗記である Aが原点となるよう3点を平行移動}すると\ {座標平面上の3点が与えられたとき四辺形の面積⃗a⃗bsinθ（θ はベクトル⃗aと⃗bの間に角）に等しい。（2） 方向と向きは、ベクトル⃗aと⃗bとに垂直で⃗aから⃗bへ右ネジを廻すときに ネジの進む方向。 その時に、次の分配法則等が成り立つ。 (1)⃗a×⃗b = −⃗b×⃗a,⃗a×⃗a = 0 (2)⃗a×(⃗b⃗c) =⃗a×⃗b⃗a×⃗c ベクトルの定番問題を一瞬で解く公式 上記と同様の議論を四面体に適用することにより以下の公式が得られます： 三角形の面積を求める公式
平行四辺形の面積 ベクトルでの公式 理数系無料オンライン学習 Kori
中1 ︎空間図形 公式一覧 中学生 数学のノート Clear 表紙 1 公開日時 16年05月07日 13時28分 更新日時 21年02月18日 17時19分 中学生 数学 「空間図形」に関連する記事の一覧です。 正三角形の面積，正四面体の体積を求める公式 (i)1辺の長さが a a a の正三角形の面積 S S S公式集：ベクトル G ベクトルと図形 G1 ベクトル G11 ベクトルの加法の基本法則 任意のベクトルa, b, c について, ① 交換法則 ab = ba ② 結合法則 (ab)c = a(b c) ③ 零ベクトルの性質 a0 = 0a = a ④ 逆ベクトルの性質 a(−a)=0,(−a)a = 0 G12 ベクトルの平行条件
中学１年数学練習問題 空間図形 切り取った立体の体積の問題
第1学年数学科学習指導案 日 時：令和 年 月 日（ ） 校時 場 所： 市立 中学校第1学年 組教室 指導者： 1 単元名（題材名） 5章 平面図形（未来へ広がる数学1 啓林館） 2 単元（題材）の目標円についての名称に関する学習です。 円はとても特殊で面白い図形なので、テストや入試にはとてもよく出題されます。 今回はその円の基本事項なので覚えるためにしっかり練習してくださいね。 中1数学 平面図形 平面図形平面図形 例題 基本の作図(垂線) 基本の作図(垂直二等分線、角の二等分線) 作図 正三角形,円の中心 作図 角度60°,30°,45° 作図 角度75° 作図 平行線 円の接線 作図 三角形の3頂点を通る円, 三角形の3辺に接する円 おうぎ形_半径と中心角から弧の長さや,面積を求める おうぎ形2_半径と弧から,面積を
おうぎ形 半径の求め方 数学の記録
次に公倍数とは 「２つ以上の整数に共通な倍数」 のことをいいます。 倍数と公倍数の大きな違いは、倍数は 1つ の整数について考えているのに対し、公倍数は 2つ 以上の整数について考えていることです。最小公倍数・倍数・公倍数③ 計算無料プリント 小学生算数問題 計算無料プリント 小学生算数問題 記事を読む最小公倍数 ご意見・ご感想 1,2,3,4,5,6,7,8,9,10,11の最小公倍数を求めるのに使用。 結果、277。 マスの数がデフォルトでは2個。マスをまとめて10個くらい追加出来ると嬉しいけど、そんな用途は少ないのかな。先日は30個以上で計算。
倍数 最小公倍数 約数 最大公約数 難しいな 7月 19年 泉小学校 ブログ 泉小学校
新しい算数 英訳版 New Mathematics for Elementary School 1①，1②，2上，2下，3上，3下，4上，4下，5上，5下，6楽しい 小学校 5年生 算数 (算数ドリル) 無料 学習アプリ 文部科学省の課程を参考にして作った小学5年生の算数勉強サポートアプリです。 小学生も簡単に操作ができるアプリです。 学習する内容ごとに細かく練習できるようになっているので、ちょっとし四谷大塚ドットコム HOME ＞ 四谷大塚 教材のご案内 ＞ 5年生教材 四谷大塚オリジナルテキスト（PDF） メイン教材 必修副教材 選択副教材 予習シリーズ 5年 予習シリーズ 計算 5年 応用演習問題集 5年 予習シリーズ 漢字とことば 5年
無料でダウンロード 算数5 年 ニスヌーピー壁紙
6/4/ ここでは整数を並べてできる3の倍数の個数を求める問題について説明します。 まず，3の倍数の見分け方を知っておこう。 3の倍数 各位の数字の和が3の倍数のとき，元の数は3の倍数である。 数学IA順列に関する問題の考え方 ここでは「順列」について説明します。順列とは，いくつかあるものを順序をつけて1列に並べる配列のことです。意味を考えて17/6/19 高校数学A 場合の数 集合の要素の個数（個数定理） 和の法則と積の法則、樹形図・表の作成による数え上げ;中学受験 5年 unit 71 場合の数1 順列と組み合わせ1 3の倍数条件は絶対に覚えておきましょう。 ご利用頂きまして誠にありがとうございます。 ご記入頂いた内容は完全に非公開です。 みんなの算数オンラインはユーザーの皆様からのすべての
数学ia 順列に関する問題の考え方 大学入試数学の考え方と解法
文字式を使った説明 問題(1 学期中間) 2 けたの正の整数がある。この整数の十の位の数と一の位の数を入れかえた2 けたの整数 をつくる。このとき，もとの整数と入れかえた整数の和は，11の倍数であることを次のよう に説明した。( )の中に適当な式や解答はこちら (1), − 2 x 9 6 (2), － b 2 (3), 59x － 40y ★「文字と式」の記事はこちらにまとめてあります↓ 『 「文字と式」を学びたいあなたはこちらをどうぞ問題まとめ 』 数学おじさん 今日のお話はこれくらいにするかのぉ 秘書ザピエル中1 学習単元一覧 正の数、負の数 文字式 方程式 関数 平面図形 空間図形 資料の整理 正の数・負の数正の数・負の数の基礎数の大小計算の基礎①計算の基礎②
無料 中２数学 発展問題 解答プリント 7 式の計算７ 文字式の利用１
→イナズマイレブンアレスの天秤 作中における「アレスの天秤」 電機メーカー「月光とても簡単で平面的な天秤座のイラスト フリーハンド 白黒 とてもシュールな天秤座 てんびん シルエット てんびん座－Libra 9/23～10/23生まれの十二星座。 12星座イラスト 天秤座から魚座までのイラスト素材 FYI。写真素材・イラスト素材のamanaimages PLUSでは、安心・安全、高品質で何度も使えるロイヤリティフリー画像素材が145円から購入いただけます。webや広告、映像の素材として最適です。 無 牡羊座 イラスト 簡単 牡羊座 イラスト 簡単14,924 一致 ページ の 150 画像の種類 ベクターイラストレーション × 白で隔離される zodiacs おとめ座 Minimal white geometric woman, zodiac sign virgo, on starry sky background 宇宙の空の背景に美しい明るい星の乙女座星座の
天秤座のイラスト素材
